Chapter 3
Multiple Linear Regression
3.1 a. 
= −1.8 + .0036
x2 + .194
x7 − .0048
x8
b. Regression is significant.

c. All three are significant.
| Coefficient |
test statistic |
p-value |
| β2 |
5.18 |
0.000 |
| β7 |
2.20 |
0.038 |
| β8 |
−3.77 |
0.001 |
d. R2 = 78.6% and R2Adj = 76.0%
e. F0 = (257.094 − 243.03)/2.911 = 4.84 which is significant at α = 0.05. The test statistic here is the square of the t-statistic in part c.
3.2 Correlation coefficient between
yi and
 i
i is .887. So (.887)
2 = .786 which is
R2.
3.3 a. A 95% confidence interval on the slope parameter β
7 is
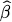 7
7 ± 2.064(.08823) = (.012, .376)
b. A 95%. confidence interval on the mean number of games won by a team when x2 = 2300, x7 = 56.0 and x8 = 2100 is
3.4 a. 
= 17.9 + .048
x7 − .00654
x8 with
F = 15.13 and
p = 0.000 which is significant.
b. R2 = 54.8% and R2Adj = 51.5% which are much lower.
c. For β7, a 95% confidence interval is 0.484 ± 2.064(.1192) ...



