Solutions Manual to Accompany Introduction to Linear Regression Analysis, 5th Edition

Chapter 13

Generalized Linear Models

13.1 a.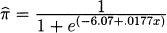

b. Deviance = 17.59 with p = 0.483 indicating that the model is adequate.

c. Ô_R = e^−.0177 = .9825 indicating that for every additional knot in speed the odds of hitting the target decrease by 1.75%.

d. The difference in the deviances is basically zero indicating that there is no need for the quadratic term.

13.3 a.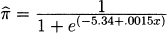

b. Deviance = .372 with p = 1.000 indicating that the model is adequate.

c. The difference in the deviances is Dev(x) − Dev(x, x²) = .372 − .284 = .088 indicating that there is no need for the quadratic term.

d. For H₀ : β₁ = 0, the Wald statistic is Z = −.42 which is not significant. For H₀ : β₂ = 0, the Wald statistic is Z = −.30 which is not significant.

e. An approximate 95% confidence interval for β₁ is (−.0018, .0033) and an approximate 95% confidence interval for β₂ is (7.15 × 10⁻⁷, 5.27 × 10⁻⁷).

13.5 a.

b. Deviance = 14.76 indicating that the model is adequate.

c. For 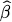₁, we get Ô_R ≈ 1 indicating that the odds are basically even. For ₁, we get Ô_R = 3.52 indicating that every one year increase in the age of the current car ...