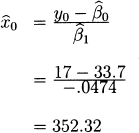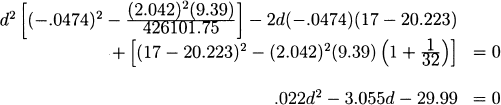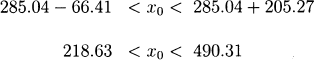March 2013
Beginner
164 pages
2h 11m
English
book
Solutions Manual to Accompany Introduction to Linear Regression Analysis, 5th Edition
by Ann G. Ryan, Douglas C. Montgomery, Elizabeth A. Peck, G. Geoffrey Vining, Anne G. Ryan
Content preview from Solutions Manual to Accompany Introduction to Linear Regression Analysis, 5th Edition
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
Chapter 15
Other Topics in the Use of Regression Analysis
15.1 It is possible, especially in small data sets, that a few outliers that follow the pattern of the “good” points can throw the fit off.
15.3 They are both oscillating functions that have similar shapes with Tukey’s bi-weight being a faster wave. However, Tukey’s bi-weight can exceed 1 while Andrew’s wave function cannot.
15.5 The fitted model is 
= 2.34 − .288x1 + .248x2 + .45x3 − .543x4 + .005x5 with a couple of outliers.
= 2.34 − .288x1 + .248x2 + .45x3 − .543x4 + .005x5 with a couple of outliers.15.7 a. The estimate is
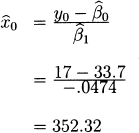
b. First we solve the following
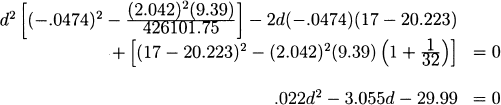
which gives d1 = −66.41 and d2 = 205.27. Then the confidence interval is
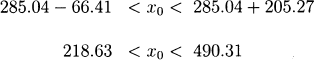
15.9 The normal-theory confidence interval for β2 is .014385±1.717(.003613) = (.0082, .0206). The bootstrap confidence interval is (.0073, .0240) which is similar to the normal-theory interval.
15.11 First, fit the model. Then, estimate the mean response at x0. Bootstrap this m times and store all of these mean responses. Finally, find the standard deviation of these responses. ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.