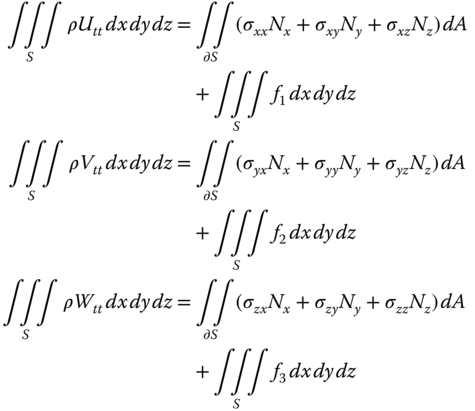5Elasticity
5.1 Derivation of Elasticity Equations
The equations that model displacements in an elastic body, such as a metal block, can be derived using Newton's second law. If we focus on an arbitrary small volume ![]() of this body and set the mass times the acceleration equal to the sum of the internal and external forces acting on
of this body and set the mass times the acceleration equal to the sum of the internal and external forces acting on ![]() , we get
, we get
Here ![]() is the density, and (
is the density, and (![]() ,
, ![]() ,
, ![]() ) is the displacement vector. That is, the body element that is at (
) is the displacement vector. That is, the body element that is at (![]() ) when the elastic body is unloaded and in equilibrium is displaced to (
) when the elastic body is unloaded and in equilibrium is displaced to (![]() , , ) at time . Thus (, , ) is the acceleration vector. The stresses are the elements ...
, , ) at time . Thus (, , ) is the acceleration vector. The stresses are the elements ...
Get Solving Partial Differential Equation Applications with PDE2D now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.