9The KPI Wave Equation1
9.1 A Difficult Nonlinear Problem
In this final chapter, we use PDE2D to solve a very challenging nonlinear problem.1
The Kadomtsev–Petviashvili I (KPI) wave equation
is used to model waves in thin films with high surface tension. It has been extensively studied in the mathematical community since the paper by Kadomtsev and Petviashvili (Kadomtsev and Petviashvili 1970). We will solve this equation using PDE2D's Galerkin method, with initial conditions consisting of two‐lump solitons, which collide and reseparate. Since the solution has steep, moving peaks, an adaptive finite element grid is used with a grading that moves with the peaks.
To use PDE2D, we have to reduce this fourth‐order equation to a system of three first‐ or second‐order equations by introducing the variables ![]() :
:
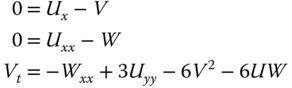
Lu, Tian, and Grimshaw (2004) give a two‐lump soliton analytical solution (astonishing that an analytical solution can be found) of the KPI equation, expressed as ![]() , where
, where ![]() is defined ...
is defined ...
Get Solving Partial Differential Equation Applications with PDE2D now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

