SQL and Relational Theory, 2nd Edition

EXERCISES

4.1 “Duplicates in databases are a good idea in because duplicates occur naturally in the real world. For example, all pennies are duplicates of one another.” How would you respond to this argument?

4.2 Let r be a relation and let bx and by be boolean expressions. Then there’s a law (used in relational systems to help with optimization, among other things) that states that (r WHERE bx) UNION (r WHERE by) ≡ r WHERE bx OR by. If r isn’t a relation but an SQL table with duplicates, does this law still apply?

4.3 Let a, b, and c be sets. Then the distributive law of intersection over union (also used in relational systems to help with optimization among other things) states that a INTERSECT (b UNION c) ≡ (a INTERSECT b) UNION (a INTERSECT c). If a, b, and c are bags instead of sets, does this law still apply?

4.4 Part of the SQL standard’s explanation of the FROM clause (as in a SELECT - FROM - WHERE expression) reads as follows:

[The] result of the <from clause> is the ... cartesian product of the tables identified by [the specifications in that <from clause>]. The ... cartesian product, CP, is the multiset of all rows r such that r is the concatenation of a row from each of the identified tables ...

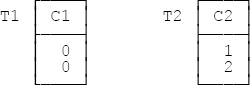
Note, therefore, that CP isn’t well defined!—the fact that the standard goes on to say that “The cardinality of CP is the product of the cardinalities of the identified tables” notwithstanding. For example, consider the tables T1 and T2 shown here:

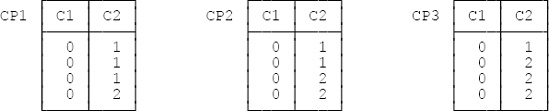
Observe now that all of the following ...