CHAPTER 3
LOCATION MODEL
Outline
3.2 Unbiased Estimates of θ and σ2 and Test of Hypothesis
3.4 Bias and MSE Expressions of the Location Estimators
3.5 Various Estimates of Variance
In this chapter, we discuss some basic results on the location model under the assumption that the error-vector is distributed according to the multivariate t-distribution.
3.1 Model Specification
Consider the location model with the response vector Y = (Y1, ···, Yn)′ such that it satisfies the relation
(3.1.1) ![]()
where 1n = (1, ···, 1)′ is an n-tuple of 1’s, and the error vector ε follows the multivariate M(n)t(0, σ2Vn γo) with pdf
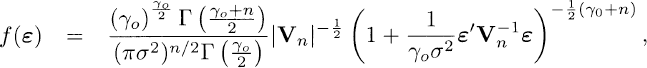
where σ > 0, Vn is a positive definite matrix of rank n and γo > 2.
The mean of ε is the zero-vector and the covariance-matrix of ε is
(3.1.2) 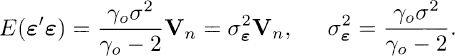
The plan of this chapter is as follows. In sections 2 and 3, unbiased estimators of θ and σ2ε are proposed along with the test statistic for testing the hypothesis H0 : θ = θ0. In addition, we propose some improved estimates of location parameter. Section 4 contains some important theorems for the bias and MSE expressions of the proposed estimators of θ and their mathematical characteristics. ...
Get Statistical Inference for Models with Multivariate t-Distributed Errors now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

