Statistical Shape Analysis, 2nd Edition

4 Shape space

In this chapter we consider the choice of shape distance, which is required to fully define the non-Euclidean shape metric space. We consider the partial Procrustes, full Procrustes and Riemannian shape distances. In the case of 2D point configurations the shape space is the complex projective space, and in the special case of triangles in two dimensions the shape space is a sphere. Finally, we consider different choices of coordinates in the tangent space to shape space, which are particularly useful for practical statistical inference.

4.1 Shape space distances

4.1.1 Procrustes distances

We shall initially describe the partial and full Procrustes distances. Consider two configuration matrices from k points in m dimensions X₁ and X₂ with pre-shapes Z₁ and Z₂. First we minimize over rotations to find the closest Euclidean distance between Z₁ and Z₂.

Definition 4.1 The partial Procrustes distance d_P is obtained by matching the pre-shapes Z₁ and Z₂ of X₁ and X₂ as closely as possible over rotations. So,

where Z_j = HX_j/||HX_j||, j = 1, 2.

Here ‘inf’ denotes the infimum, and we will use ‘sup’ for the supremum.

Result 4.1 The partial Procrustes distance is given by:

(4.1)

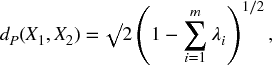
where λ₁ ≥ λ₂ ≥ … ≥ λ_{m − 1} ≥ |λ_m| are the square roots of the eigenvalues of Z^T₁Z₂Z^T₂Z₁, ...