Statistical Thermodynamics

7Imperfect Gas

In this chapter, we employ the canonical‐ensemble formulation to take into account interactions between molecules in a gas. We have found molecular‐level expressions of the interaction in Section 3.4. We use them to derive the equation of state similar to that of van der Waals gas.

7.1 Virial Expansion

The equation of state for a perfect gas is pV = Nk_BT. We have proved in Section 4.6 that a canonical ensemble of noninteracting molecules gives this equation of state. In real gas, the interactions are always present. At low pressures, the effect of the interactions on the equation of state is negligible, since the interactions are much smaller compared with the other components of energy. With an increasing pressure, the interactions become a larger part of the total energy. We cannot neglect the interactions any more.

A deviation from the ideality is represented in the virial expansion:

7.1

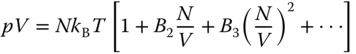
It is an expansion of pV/(Nk_BT) by the number density N/V (number of molecules in unit volume). The expansion coefficients are called virial coefficients; in increasing order, the second virial coefficient (B₂), the third virial coefficient (B₃), and so on. They are constants of N/V. In the low‐density limit, the equation reduces to the equation of state of the perfect gas. The reason why the coefficients are called second, third, etc. – not first, second, etc. – will be clear, ...