Statistical Thinking: Improving Business Performance, Second Edition

APPENDIX G

More on Probability Distributions

Probabilities direct the conduct of the wise man.

—Cicero

This appendix will briefly review the concept of a probability distribution (presented in Chapter 9) and then present summary information (formulas, averages, and variances) on several common continuous and discrete distributions. Typical applications of these distributions will also be noted. For more information on probability distributions, see Walpole, Myers, Myers, and Ye.1

DISCRETE PROBABILITY DISTRIBUTIONS

Discrete probability distributions, also called probability mass functions, quantify the probability of each possible outcome for a discrete random variable. For example, we might wish to calculate the probability of winning 0, 1, or 2 bids when submitting 2 bids for different municipal bonds.

Some rules about basic probability:

• Each individual probability must be somewhere between 0 and 1, where 0 means the outcome is not possible and 1 means that the outcome is certain. Let’s suppose the probability of winning a given bid is .5.
• The sum of probabilities for all possible outcomes must equal 1. For example, if the probability of winning 0 bids is .25, and the probability of winning 1 is .5, then the probability of winning 2 must be .25.
• The probability of two events, A and B, both occurring (the intersection), is 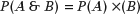assuming A and B are independent of one another. For example, ...