April 2014
Intermediate to advanced
736 pages
20h 32m
English
Content preview from Statistics: Principles and Methods, 7th Edition
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
APPENDIX A2
Rules for Counting
Some basic rules for counting can help us calculate probabilities. We begin with an example. Brazil (B), United States (U.S.), Mexico (M), Canada (C), and Japan (J) are in the final round of a volleyball tournament. How many ways can a winner and second place finisher be selected?
To systematically address this problem, we create a tree diagram where the possibilities for first place are represented by the initial 5 branches. For each choice of a first place finisher, there are four choices for second place. These are represented by the sets of 4 branches in the second stage. For instance, the leftmost branch of the tree diagram depicts the case where Brazil is first and the United States second and so on.
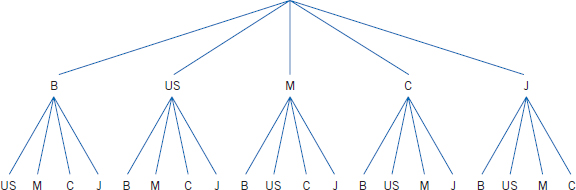
There are 5 × 4 = 20 terminal points or ways for these teams to finish first and second. Generalizing the tree diagram to k choices followed by m choices, we obtain the product rule for counting.
Product Rule
An experiment consists of two parts where the first part has k distinct possible outcomes and, for each outcome of the first part, there are m distinct possible outcomes for the second part. Then, there are k × m distinct possible outcomes to the experiment.
The product rule is readily extended to experiments with more than two parts. Suppose we are interested in the winner, second, and third place finishers in the volleyball tournament. ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.