April 2014
Intermediate to advanced
736 pages
20h 32m
English
Content preview from Statistics: Principles and Methods, 7th Edition
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
APPENDIX A3
Expectation and Standard Deviation—Properties
The expected value of a discrete random variable is a summation of the products (value × probability). The key properties of expectations are then all inherited from the properties of summation. In this appendix, we indicate this development for some of the most useful properties of expectation and variance. The interested reader can consult Bhattacharyya and Johnson1 for more details.
A3.1 EXPECTED VALUE AND STANDARD DEVIATION OF cX + b
The units of the random variable X may be changed by multiplying by a constant, for example,
or by adding a constant, for example,
The mean and standard deviation of the new random variables are related to μ = E (X) and σ = sd (X).
If X is multiplied by a constant c,
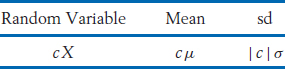
If a constant b is added to X,
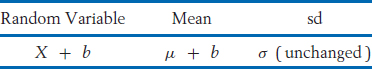
Notice that adding a constant to a random variable leaves the standard deviation unchanged.
Example
Let X have mean = 3 = μ and standard deviation = 5 = σ. Find the mean and sd of (a) X + 4, (b) 2X, (c) −X, and (d) .
SOLUTION
By the foregoing properties,
Finally, (X − 3) has mean 3 − 3 = 0 and sd ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.