Stochastic Geometry for Image Analysis

Chapter 2

Marked Point Processes for Object Detection 1

In this chapter we introduce the essential concepts that define a marked point process. Only the tools that are necessary for image analysis problems are presented. A detailed description of point processes can be found in [STO 95, BAR 99, LIE 00].

2.1. Principal definitions

Consider K, a compact subset of represents the image support, that is, the image coordinates are projected in a continuous space. A configuration of points, denoted by x, is a finite unordered set of points in K, such as {x1, … xn}. The configuration space, denoted by Ω, is therefore written as:

where Ω0 = {∅} and Ωn = {{x1, …, xn}, Xi ∈ K, ∀i} is the set of the configurations of n unordered points for n ≠ 0. We will use the Lebesgue measure on K, written as Λ(K), to measure the configuration space. Given that we are working with unordered sets of points, we can therefore measure Ω as follows:

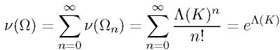
Let be a probability space, and let X be an application of to Ω. ...