Stochastic Modeling and Analysis of Telecoms Networks

Appendix AMathematical Toolbox

 

 

 

Mathematical concepts and theorems have their existence and their own interests. As regards modeling, mathematics mainly become a toolbox to solve practical problems. To make good food, it still necessary to know the ingredients available. We review in this chapter the mathematical theorems used in the rest of this book.

A.1. Probability spaces and processes

A.1.1. Countable spaces

The concept of countability plays an important role in probability if only because the property of measurability is stable only by countable union. It is therefore interesting to clarify some results related to this concept.

DEFINITION A.1.– A set E is a finite cardinal with n elements if there exists a bijection from E into the set {1, …, n}.

DEFINITION A.2.– A set E is called countable (or countably infinite) if there exists a bijection from E into N, the set of natural integers.

EXAMPLE. – 2N, the set of integers is countable. (N), set of subsets of N, is not since it can be bijectively mapped to the set of real numbers R. Indeed, for a subset A of N, we can define a sequence by

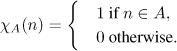
Then, with this sequence, we can associate the real number x_A defined by x_A = . In the ...