Student Solutions Manual Applied Statistics and Probability for Engineers, Fifth Edition

CHAPTER 10

Section 10-2

10-1.    a)   1)   The parameter of interest is the difference in means μ₁ – μ₂. Note that Δ_{0 =} 0.

2)   H₀ : μ₁ – μ₂ = 0 or μ₁ = μ₂

3)   H₁ : μ₁ – μ₂ ≠ 0 or μ₁ ≠ μ₂

4)   The test statistic is

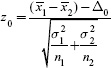
5)   Reject H₀ if z₀ < –z_α/2 = –1.96 or z₀ > z_α/2 = 1.96 for α = 0.05.

6)   ₁ = 4.7    ₂ = 7.8

σ₁ = 10        σ₂ = 5

n₁ = 10          n₂ = 15

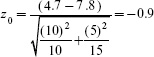
7)   Conclusion: Because –1.96 < –0.9 < 1.96, do not reject the null hypothesis. There is not sufficient evidence to conclude that the two means differ at α = 0.05.

           P-value = 2(1 – Φ(0.9)) = 2(1 – 0.8 159 50) = 0.36 8

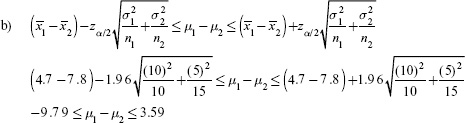
With 95% confidence, the true difference in the means is between –9.79 and 3.59. Because zero is contained in this interval, we conclude there is no significant difference between the means. We fail to reject the null hypothesis.

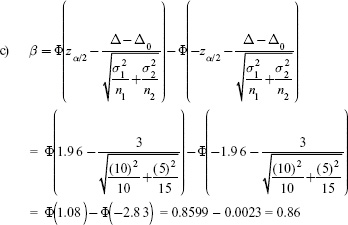
Power = 1 – 0.86 = 0.14

d)   Assume the sample sizes are to be equal, use α = 0.05, ...