CHAPTER 6
CHAPTER 6 SOLUTIONS
6.1 SECTION 6.1
6.1
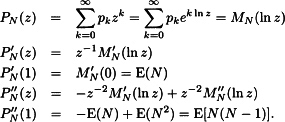
6.2 SECTION 6.5
6.2 For Exercise 14.3, the values at k = 1, 2, 3 are 0.1000, 0.0994, and 0.1333, which are nearly constant. The Poisson distribution is recommended. For Exercise 14.5, the values at k = 1, 2, 3, 4 are 0.1405, 0.2149, 0.6923, and 1.3333, which is increasing. The geometric/negative binomial is recommended (although the pattern looks more quadratic than linear).
6.3 For the Poisson, λ > 0 and so it must be a = 0 and b > 0. For the binomial, m must be a positive integer and 0 < q < 1. This requires a < 0 and b > 0 provided −b/a is an integer ≥ 2. For the negative binomial, both r and β must be positive so a > 0 and b can be anything provided b/a > −1.
The pair a = −1 and b = 1.5 cannot work because the binomial is the only possibility but −b/a = 1.5, which is not an integer. For proof, let p0 be arbitrary. Then p1 = (−1 + 1.5/1)p = 0.5p and p2 = (−1 + 1.5/2)(0.5p) = −0.125p < 0.
6.3 SECTION 6.6
6.4
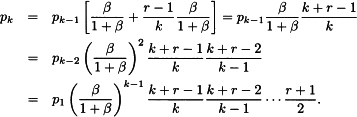
The factors will be positive (and thus pk will be positive) provided p1 > 0, β > 0, r > −1, and r ≠ 0.
To see that the probabilities sum to a finite amount,
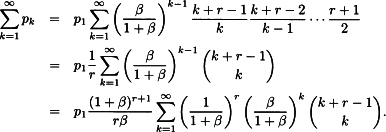
The terms of the summand are the pf of the negative binomial ...
Get Student Solutions Manual to Accompany Loss Models: From Data to Decisions, Fourth Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

