Student Solutions Manual to Accompany Loss Models: From Data to Decisions, Fourth Edition

CHAPTER 18

CHAPTER 18

18.1   SECTION 18.9

18.1 The conditional distribution of X given that Y = y is

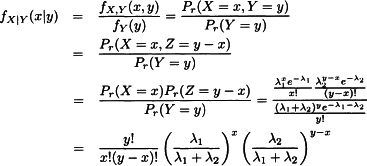
for x = 0, 1, 2,…, y. This is a binomial distribution with parameters m = y and q = λ₁/(λ₁ + λ₂).

18.2

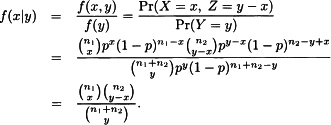
This is the hypergeometric distribution.

18.3 Using (18.3) and conditioning on N yields

For the variance, use (18.6) to obtain

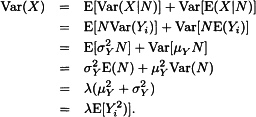
18.4 (a) f_X(0) = 0.3, f_X(1) = 0.4, f_X(2) = 0.3.

      f_Y(0) = 0.25, f_Y(1) = 0.3, f_Y(2) = 0.45.

(b) The following array presents the values for x = 0, 1, 2:

(c)

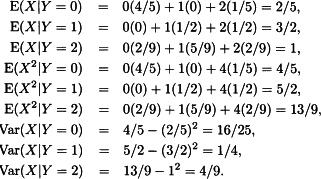
(d)

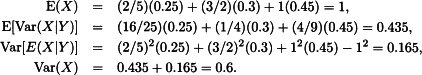
18.5 (a)

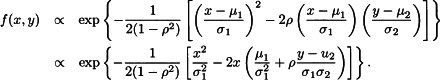
Now a normal density N(μ, σ²) has pdf . Then f_X|Y(x|y) ∝ f(x, y) is N  .

(b)