Indefinite Integrals of Elementary Functions
2.0 Introduction
2.00 General remarks
We omit the constant of integration in all the formulas of this chapter. Therefore, the equality sign (=) means that the functions on the left and right of this symbol differ by a constant. For example (see integral 2.01 15), we write
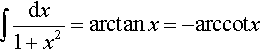
although
![]()
When we integrate certain functions, we obtain the logarithm of the absolute value In such formulas, the absolute-value ...
Get Table of Integrals, Series, and Products, 8th Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

