2.4 Hyperbolic Functions
2.41–2.43 Powers of sinh x, cosh x, tanh x, and coth x
2.411 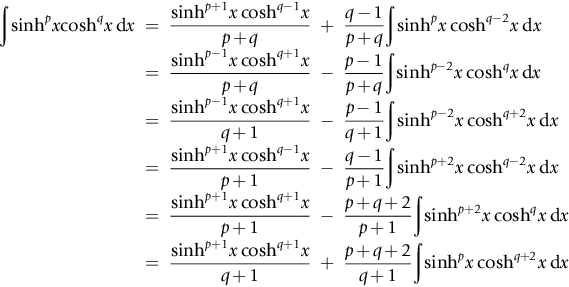
2.412
1.
This formula is applicable for arbitrary real p except for the following negative even integers: ...
Get Table of Integrals, Series, and Products, 8th Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

