“Approximation by tangents”
8.45211 For large values of the index (where the argument is less than the index).
Suppose that x < 0 and ν < 0. Let us set ν/x = cosh α. Then, for large values of ν, the following expansions are valid:
1.
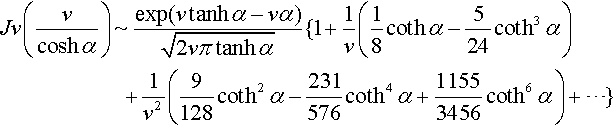 WA 269(3)
WA 269(3)
2.
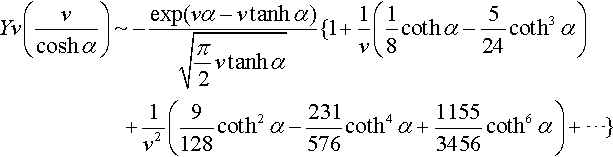 WA 270(5)
WA 270(5)
8.453 For large values of the index (where the argument is greater than ...
Get Table of Integrals, Series, and Products, 8th Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

