Integral Inequalities
11.11 Mean Value Theorems
11.111 First mean value theorem
Let f(x) and g(x) be two bounded functions integrable in [a, b] and let g(x) be of one sign in this interval. Then
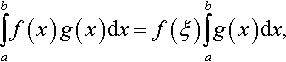 CA 105
CA 105
with a ≤ ξ ≤ b.
11.112 Second mean value theorem
(i) Let f(x) be a bounded, monotonic decreasing, and nonnegative function in [a, b], and let g(x) be a bounded integrable function. Then,
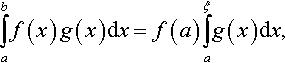
with a ≤ ξ ≤ b.
(ii) Let f(x) be a bounded, monotonic increasing, and nonnegative function ...
Get Table of Integrals, Series, and Products, 8th Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

