Table of Integrals, Series, and Products, 8th Edition

0.3 Functional series

0.30 Definitions and theorems

0.301 The series

1. 

${\displaystyle \sum _{k=1}^{\infty }{f}_k}\left(x\right),$

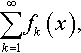
the terms of which are functions, is called a functional series. The set of values of the independent variable x for which the series 0.301 1 converges constitutes what is called the region of convergence of that series.

0.302 A series that converges for all values of x in a region M is said to converge uniformly in that region if, for every e = 0, there exists a number N such that, for n > N, the inequality

$\left|{\displaystyle \sum _{k=n+1}^{\infty }{f}_k}\left(x\right)\right|<\epsilon$

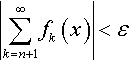
holds for all x in M.

0.303 ...