Technical Mathematics, Sixth Edition

19.5. Alternating Current Applications

19.5.1. Rotating Vectors in the Complex Plane

We have already shown that a vector can be represented by a complex number. For example, the complex number represents a vector of magnitude 5.00 at an angle of 28° with the real axis.

Glance back to Chap. 15 where we first introduced alternating current.

A phasor (a rotating vector) may also be represented by a complex number by replacing the angle θ by ωt where ω is the angular velocity and t is time.

Example 32: The complex number represents a phasor of magnitude 11 rotating with an angular velocity of 5 rad/s.

Figure 19.12. FIGURE 19-12

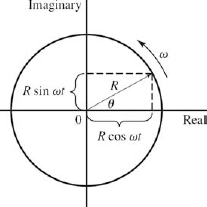
In Sec. 15–3 we showed that a phasor of magnitude R has a projection on the y axis of R sin ωt. Similarly, a phasor in the complex plane (Fig. 19-12) will have a projection on the imaginary axis of R sin ωt. Thus

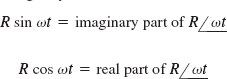
Similarly,

Thus either a sine or a cosine wave ...