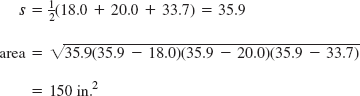8.5. Applications
As with right triangles, oblique triangles have many applications in technology, as you will see in the exercises for this section. Follow the same procedures for setting up these problems as we used for other word problems, and solve the resulting triangle by the law of sines or the law of cosines, or both.
If an area of an oblique triangle is needed, either compute all the sides and use Hero's formula (Eq. 103), or find an altitude with right-triangle trigonometry and use Area = ![]() (base)(altitude).
(base)(altitude).
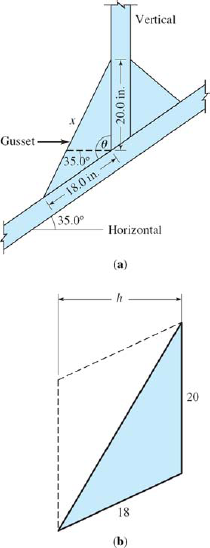
Example 29:Find the area of the gusset in Fig. 8-38(a). Solution: We first find θ.
We now know two sides and the angle between them, so can find side x by the law of cosines.
Finally we find the area of the gusset by Hero's formula (Eq. 103).
Check: Does the answer look reasonable? Let's place the gusset inside the parallelogram, as shown in Fig. 8-38(b), and estimate the height h by eye at about 15 in. Thus the area of the parallelogram would be 15 × 20 or 300 in.2, just double that found for the triangle. |
Figure 8.38. FIGURE 8-38
Example ... |
Get Technical Mathematics, Sixth Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.