Technical Mathematics, Sixth Edition

22.2. Equation of a Straight Line

We said earlier that one value of analytic geometry was the ability to write an equation for a geometric figure. Then we could analyze that figure using algebra. Here we will write an equation for a geometric figure, the straight line. Such an equation would relate y to x for any point on the figure, so that given one coordinate, we could find the other from the equation.

22.2.1. Slope-Intercept Form

We covered the slope-intercept form of the equation of a straight line in our chapter on graphing, and we will repeat some of that material here. We will also show a few other forms of the straight line equation.

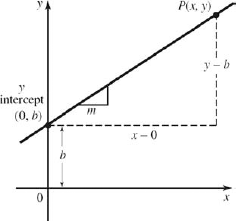
One way we can get such an equation is from our definition of slope. Let P(x, y) be any point on a line, Fig. 22-20, and let the y intercept, (0, b) be a second point on the line. Between P and the y intercept, the rise is (y − b) and the run is (x − 0). The slope m of the line is then

Simplifying, we have mx = y − b, or

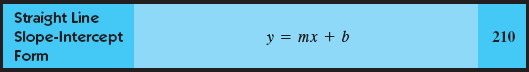
Figure 22.20. FIGURE 22-20

This is called the slope-intercept form of the equation of a straight line because the slope m and the y intercept b are easily identified once the equation is in this form. For example, in the ...