Technical Mathematics, Sixth Edition

16.3. Functions of Double Angles and Half-Angles

We come now to our last batch of identities, those involving two times an angle and those involving half an angle.

16.3.1. Functions of Double Angles

▪ Exploration:

Is the sine of twice an angle equal to twice the sine of that angle? Is sin 2α = 2 sin α? Try this: By calculator, evaluate

sin 2(40°) 2 sin(40°)

Are these equal? Try it again with other angles. Try it for the cosine and tangent. What do you conclude?

NOTE

The sine of twice an angle is not twice the sine of the angle. Nor is the cosine (or tangent) of twice an angle equal to twice the cosine (or tangent) of that angle.

Remember to use the formulas from this section for all of the trig functions of double angles.

16.3.2. Sine of Twice an Angle

An equation for the sin 2α may be derived by setting β = α in the identity for sin(α + β).

sin(α + α) = sin α cos α + cos α sin α

which we can rewrite as:

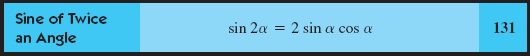
16.3.3. Cosine of Twice an Angle

Similarly, setting β = α in the identity for cos(α + β) gives

cos(α + α) = cos α cos α − sin α sin α

which can also be written,

NOTE

There are two alternative forms to this identity. Since sin²α + cos²α = 1,

cos²α = 1 − sin²α

Substituting yields

cos 2α = 1 − sin²α − sin²α

Thus,

NOTE

Similarly, we can use the same identity, sin²α + cos