Technical Mathematics, Sixth Edition

15.5. Graphing a Parametric Equation

For the equations we have graphed so far, in rectangular coordinates, y has been expressed as a function of x.

y = f(x)

But x and y can also be related to each other by means of a third variable, say, t, if both x and y are given as functions of t.

x = g(t)

and

y = h(t)

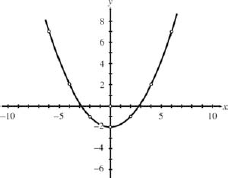
Figure 15.29. FIGURE 15-29

Such equations are called parametric equations. The third variable t is called the parameter.

To graph parametric equations, we assign values to the parameter t and compute x and y for each t. We then plot the table of (x, y) pairs.

Example 24: Graph the parametric equations x = 2t and y = t2 − 2 for t = −3 to 3. Solution: We make a table with rows for t, x, and y. We take values of t from −3 to 3, and for each we compute x and y. t −3 −2 −1 0 1 2 3 x −6 −4 −2 0 2 4 6 y 7 2 −1 −2 −1 2 7 We now plot the (x, y) pairs, (−6, 7), (−4, 2), ..., (6, 7) and connect them with a smooth curve (Fig. 15-29). The curve obtained is a parabola, the same curve we graphed in an earlier chapter, but obtained here with parametric equations.

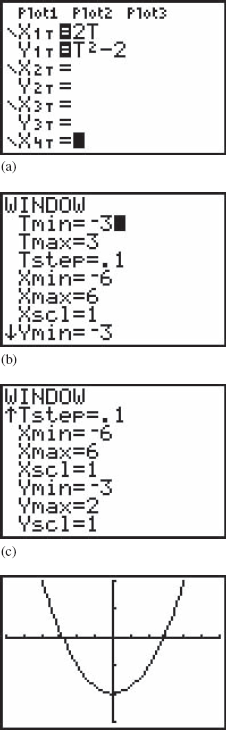
(d) Graph of x = 2t and y = t² − 2. Tick marks are 1 unit apart on both axes.

15.5.1. Graphing Parametric Equations by Calculator

We will show how to do this with an example.

Example 25: Repeat Example 23 by calculator. Solution: We first set the calculator ...