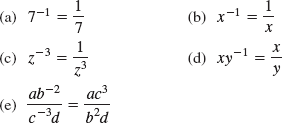13.1. Integral Exponents
In this section, we continue the study of exponents that we started in Chap. 2. We repeat the laws of exponents derived there and use them to simplify more difficult expressions than before. You should glance back at that section before starting here.
13.1.1. Negative Exponents
The law that we derived in Chap. 2 for a negative exponent is repeated here.
NOTE
![]()
When taking the reciprocal of a base raised to a power, change the sign of the exponent.
We'll use the laws of exponents mainly to simplify expressions, to make them easier to work with in later computations, such as solving equations containing exponents. For example, we use the law for negative exponents to rewrite an expression so that it does not contain a negative exponent.
Example 1:In these examples we use Eq. 28 to eliminate negative exponents.
|
NOTE
- x−a ≠ x1/a
13.1.2. Integral Exponents by Calculator
A calculator that can do symbolic algebra may be used to simplify expressions containing exponents. On the TI-89, we use expand from the Algebra menu.
Example 2:Simplify the expression from Example 1(d),
Solution: We choose expand and enter the expression as shown. Pressing |
Get Technical Mathematics, Sixth Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.