Technical Mathematics, Sixth Edition

8.4. Law of Cosines

To use the law of sines we need a known side opposite a known angle. Sometimes we do not have that information, as when, for example, we know three sides and no angle. We can still solve such a triangle using the law of cosines.

8.4.1. Derivation

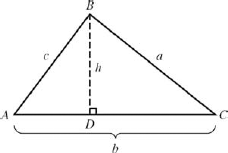
Consider an oblique triangle ABC as shown in Fig. 8-27. As we did for the law of sines, we start by dividing the triangle into two right triangles by drawing an altitude h to side AC.

In right triangle ABD,

c² = h² + (AD)²

But AD = b − CD. Substituting, we get

Now, in right triangle BCD, by the definition of the cosine,

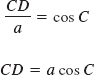
or

Substituting a cos C for CD in Equation (1) yields

c² = h² + (b − a cos C)²

Squaring, we have

Figure 8.27. Derivation of the law of cosines.

Let us leave this expression for the moment and write the Pythagorean theorem for the same triangle BCD.

h² = a² − (CD)²

Again substituting a cos C for CD, we obtain

Substituting this expression for h² back into (2), we get

c¹ = a² − a²cos²C + b² − 2ab cos ...