14.1. Radian Measure
▪ Exploration:
Try this. (a) Make a photocopy of a protractor, Fig. 14-2. (b) Cut a strip of paper whose length equals the radius of the protractor circle. (c) Starting at 0°, bend the strip around the edge of the protractor and mark its end point (this will be easier if you paste the photocopy to cardboard and cut it out). (d) Draw a line from the end of the strip to the center O, forming angle θ.
What is the significance of θ? About how large is θ in degrees? Estimate roughly how many angles of size θ will fit completely around the circle.
Figure 14.2. FIGURE 14-2
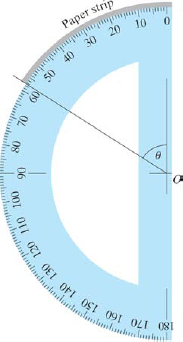
The angle θ you constructed in the exploration is defined as one radian. A radian is the central angle subtended by an arc whose length is one radius, Fig. 14-3.
We will see that the radian is a dimensionless ratio and not a unit of measure like the degree or the inch. Thus it is not strictly correct to write "radians" after the angle, but we will do so anyway because it makes it easier to keep track of our angles during a computation.
14.1.1. Angle Conversion
By definition, an arc having a length equal to the radius of the circle subtends a central angle of one radian. It follows that an arc having a length of twice the radius subtends a central angle of two radians, and so on. Thus an arc with a length of 2π times the radius (the entire circumference) subtends a central angle of 2π radians. ...
Get Technical Mathematics, Sixth Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

