Technical Mathematics, Sixth Edition

13.2. Simplification of Radicals

Here we will review and expand upon material first given in earlier chapters. Recall that a radical consists of a radical sign, a quantity under the radical sign called the radicand, and the index of the radical.

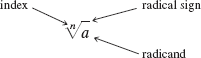
where n is an integer. For now we will restrict the radicand to a positive number when the index is even. We will consider even roots of negative numbers when we cover imaginary numbers.

13.2.1. Relation between Fractional Exponents and Radicals

We have seen that when a number, say 5, is multiplied by itself

5 × 5 = 25

then 5 is called the square root of 25.

In other words, when two equal factors are multiplied together, one of these factors is the square root of the product. Let us try this with the number a^1/2.

Here we have two equal factors, a^1/2, and a^1/2, multiplied together, so one of these factors is the square root of the product a.

NOTE

Raising to an exponent 1/2 means the same as taking the square root. Recall that we used this relation in Chap. 1 to take the root of a number using a calculator that did not have keys for taking roots.

Example 13: Some expressions with fractional exponents are rewritten here as radicals.