Technical Mathematics, Sixth Edition

10.2. Solving Systems of Equations by the Unit Matrix Method

This method is perhaps the fastest and easiest way to solve a set of equations by calculator. We will show it for a set of three equations, but it can be used for any number of equations.

Let us solve a system of equations by the addition-subtraction method given in Chap. 9. At the same time we will show a matrix of the coefficients and the column of constants to the right of the equations.

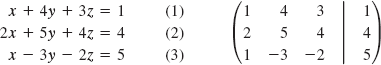
First we multiply Eq. 1 by 2 and subtract it from Eq. 2. We also subtract Eq. 1 from Eq. 3. We get

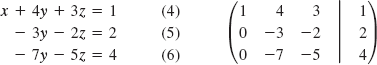
Next we multiply Eq. 5 by and add the result to Eq. 4. We also multiply Eq. 5 by and add the result to Eq. 6.

Finally, we multiply Eq. 9 by −3, getting z = 2 (Eq. 12). Then we use Eq. 12 to eliminate z from Eqs. 7 and 8.

Our solution is then

x = 3; y = −2; z = 2

Now notice the final matrix. The square matrix made up of the coefficients of the variables has 1's along the main diagonal and zeros elsewhere. This we had earlier defined as a unit matrix. Thus if we transform our original matrix of the coefficients into a unit matrix, then the ...