Technical Mathematics, Sixth Edition

22.3. The Circle

22.3.1. The Conic Sections

We turn now from the straight line to a very interesting group of curves called the conic sections: the circle, ellipse, parabola, and hyperbola.

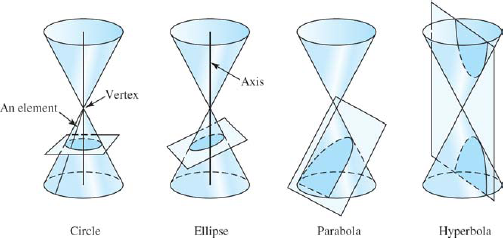
A circular conical surface is one swept out by a line which is fixed at a point (the vertex) as another point on that line follows a circular path. This gives an upper and lower cone, called nappes, such as those we studied in our chapter on geometry. The conic sections are obtained by passing a plane through a circular conical surface, as shown in Fig. 22-36.

The great Greek geometer Apollonius of Perga (c. 255–170 B.C.E.) is credited as the first to define the conic sections in this way.

When the plane is perpendicular to the cone's axis, it intercepts a circle. When the plane is tilted a bit, but not so much as to be parallel to an element (a line on the cone that passes through the vertex) of the cone, we get an ellipse. When the plane is parallel to an element of the cone, we get a parabola, and when the plane is steep enough to cut the upper cone, we get the two-branched hyperbola.

▪ Exploration:

Try this. Make a model of the conic sections. Construct a cone (from clay, styrofoam, plaster poured into a conical cardboard mold, a wood turning, etc.) and cut it as shown to form any of the four curves.

Figure 22.36. Conic sections.

22.3.2. Definition of a Circle

Our first conic section ...