Technical Mathematics, Sixth Edition

22.5. The Ellipse

22.5.1. Definition of the Ellipse

Our third conic is the ellipse, another curve that has many applications. As we said, it is formed when a cone is cut by a plane that is not perpendicular to the cone's axis but is not tilted so much as to be parallel to an element of the cone. We also define an ellipse as a set of points meeting the following conditions:

NOTE

An ellipse is the set of all points in a plane such that the sum of the distances from each point 229 on the ellipse to two fixed points (called the foci) is constant.

▪ Exploration:

Try this. Push two tacks into a drafting board, spaced by about 6 inches apart, Fig. 22-71. Pass a loop of string around the tacks, pull it taut with a pencil, and trace a curve.

Figure 22.71. Construction of an ellipse.

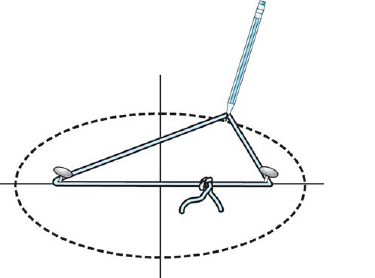
The curve you got was apparently an ellipse. Comparing your construction with the definition above, can you say whether your ellipse is exact or approximate?

Now measure half the distance between the tacks, half the long dimension of your ellipse, and half the short dimension. Can you see how those three half-dimensions are related? Change the distance between the tacks, retie the string, and draw another ellipse. Does your relationship between the three half-dimensions still hold?

Figure 22.72. Ellipse.

Figure 22-72 shows the typical shape of the ellipse. An ellipse has two axes of symmetry: the major ...