Technical Mathematics, Sixth Edition

22.4. The Parabola

Our second conic section is the parabola. It is another amazing curve, describing the deflection of beams, the path of objects thrown or dropped, and the orbits of some comets. It is used in the design of optical devices, highway curves, and much more.

22.4.1. Definition of a Parabola

We said that the parabola results when we cut a cone by a plane that is parallel to an element of the cone. Here is another definition.

Figure 22.48. Construction of a parabola.

NOTE

A parabola is the set of points in a plane, each of which is equidistant from a fixed point, the focus, and a fixed line, the directrix.

▪ Exploration:

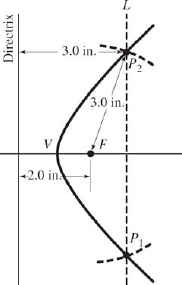
Try this. Use the preceding definition to construct a parabola whose distance from focus to directrix is 2.0 in.

(a) Draw a line to represent the directrix as shown in Fig. 22-48, and indicate a focus F 2.0 in. from that line. (b) Then draw a line L parallel to the directrix at some arbitrary distance, say, 3.0 in. (c) With the same (3.0-in.) distance as radius and F as center, use a compass to draw arcs intersecting L at P₁ and P₂. Each of these points is now at the same distance (3.0 in.) from F and from the directrix and is hence a point on the parabola. (d) Repeat the construction with distances other than 3.0 in. to get more points on the parabola.

Figure 22-49 shows the typical shape of a parabola. The parabola has an axis of symmetry which ...