Technical Mathematics, Sixth Edition

5.4. The Straight Line

We already learned how to graph any equation, including that for a straight line, by computing and plotting a set of point pairs. But by looking for special features on some curves, such as the straight line and the parabola, our work gets much easier. We will give just an introduction to the straight line here, and we will examine it and the parabola in more detail in our chapter on analytic geometry.

5.4.1. Slope

As a particle moves from point P, Fig. 5-13, to point Q, the horizontal distance moved is called the run, and the increase or decrease of the vertical distance between the same points is called the rise. For points P and Q in Fig. 5-13, the rise is 6 in a run of 3. The rise divided by the run is called the slope of the line and is usually denoted by the letter m.

Example 14: The slope of the line in Fig. 5-13 is

Figure 5.13. FIGURE 5-13

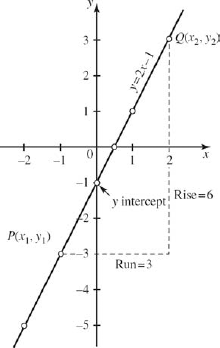
We can find the slope if given the coefficients of two points on the line. Let the two points be P(x₁, y₁) and Q(x₂, y₂) as shown in Fig. 5-13. Then the rise from P to Q is y₂ − y₁ in a run of x₂ −x₁. As before, the slope m is the rise divided by the run, so,

NOTE

The slope of a straight line equals its rise, ...