Chapter 4. Fully Connected Deep Networks
This chapter will introduce you to fully connected deep networks. Fully connected networks are the workhorses of deep learning, used for thousands of applications. The major advantage of fully connected networks is that they are “structure agnostic.” That is, no special assumptions need to be made about the input (for example, that the input consists of images or videos). We will make use of this generality to use fully connected deep networks to address a problem in chemical modeling later in this chapter.
We delve briefly into the mathematical theory underpinning fully connected networks. In particular, we explore the concept that fully connected architectures are “universal approximators” capable of learning any function. This concept provides an explanation of the generality of fully connected architectures, but comes with many caveats that we discuss at some depth.
While being structure agnostic makes fully connected networks very broadly applicable, such networks do tend to have weaker performance than special-purpose networks tuned to the structure of a problem space. We will discuss some of the limitations of fully connected architectures later in this chapter.
What Is a Fully Connected Deep Network?
A fully connected neural network consists of a series of fully connected layers. A fully connected layer is a function from to . Each output dimension depends on each input dimension. Pictorially, a fully connected layer is represented as follows in Figure 4-1.
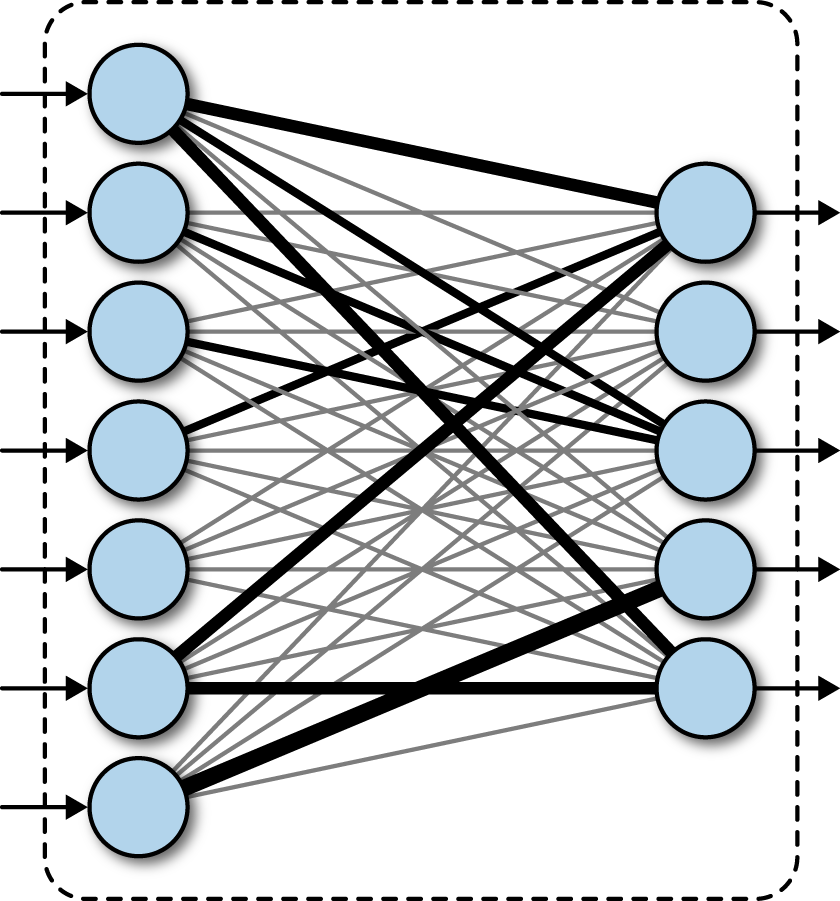
Figure 4-1. A fully connected layer in a deep network.
Let’s dig a little deeper into what the mathematical form of a fully connected network is. Let represent the input to a fully connected layer. Let be the -th output from the fully connected layer. Then is computed as follows:
Here, is a nonlinear function (for now, think of as the sigmoid function introduced in the previous chapter), and the are learnable parameters in the network. The full output y is then
Note that it’s directly possible to stack fully connected networks. A network with multiple fully connected networks is often called a “deep” network as depicted in Figure 4-2.
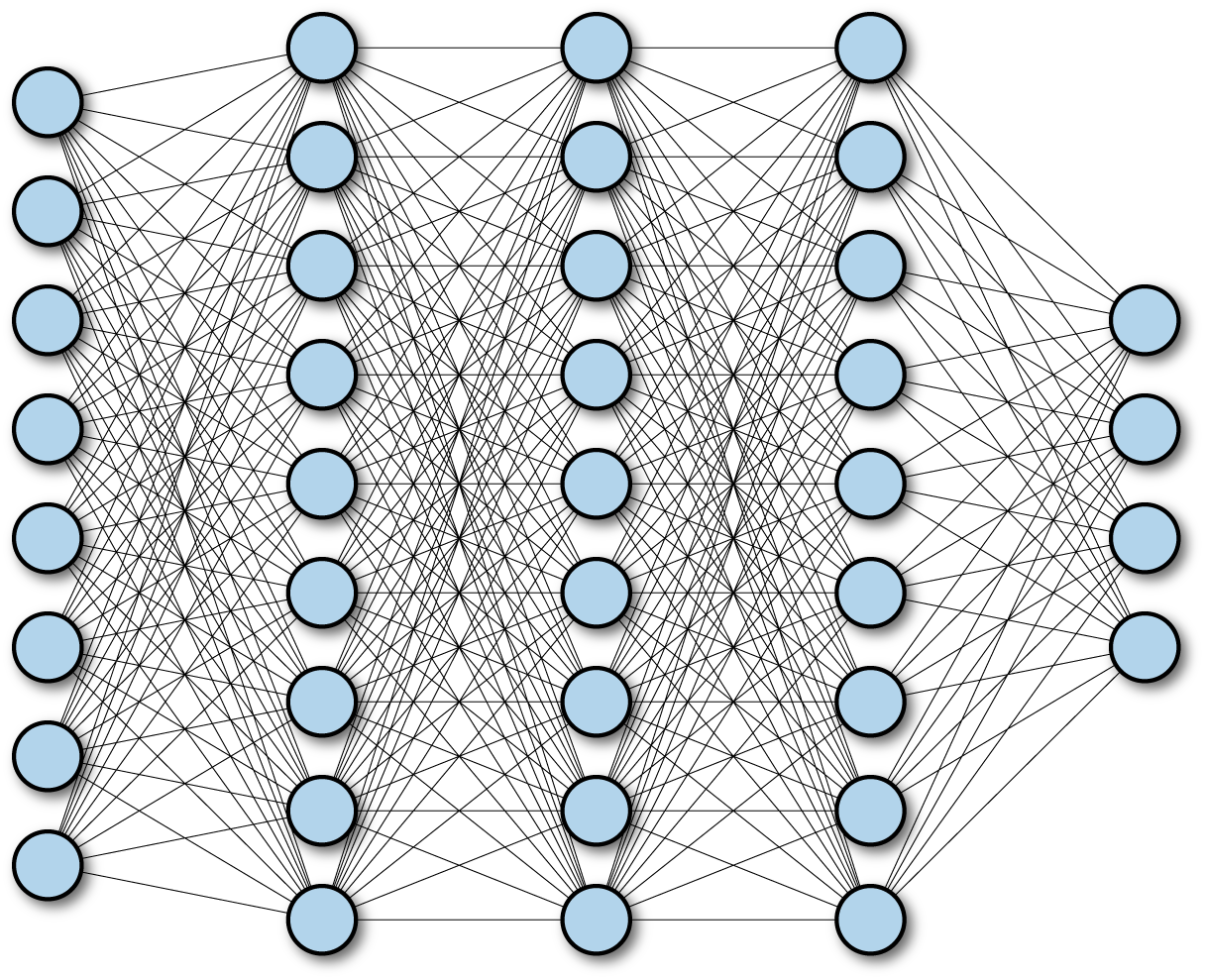
Figure 4-2. A multilayer deep fully connected network.
As a quick implementation note, note that the equation for a single neuron looks very similar to a dot-product of two vectors (recall the discussion of tensor basics). For a layer of neurons, it is often convenient for efficiency purposes to compute y as a matrix multiply:
where sigma is a matrix in and the nonlinearity is applied componentwise.
“Neurons” in Fully Connected Networks
The nodes in fully connected networks are commonly referred to as “neurons.” Consequently, elsewhere in the literature, fully connected networks will commonly be referred to as “neural networks.” This nomenclature is largely a historical accident.
In the 1940s, Warren S. McCulloch and Walter Pitts published a first mathematical model of the brain that argued that neurons were capable of computing arbitrary functions on Boolean quantities. Successors to this work slightly refined this logical model by making mathematical “neurons” continuous functions that varied between zero and one. If the inputs of these functions grew large enough, the neuron “fired” (took on the value one), else was quiescent. With the addition of adjustable weights, this description matches the previous equations.
Is this how a real neuron behaves? Of course not! A real neuron (Figure 4-3) is an exceedingly complex engine, with over 100 trillion atoms, and tens of thousands of different signaling proteins capable of responding to varying signals. A microprocessor is a better analogy for a neuron than a one-line equation.
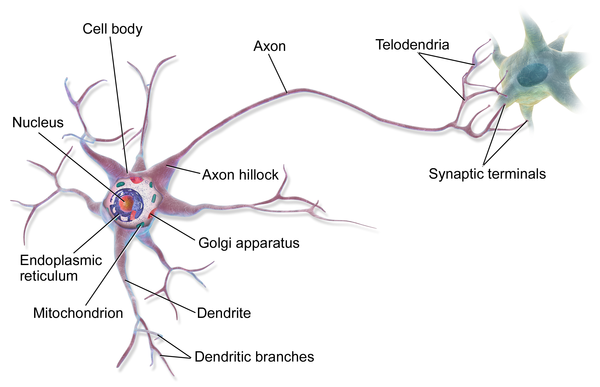
Figure 4-3. A more biologically accurate representation of a neuron.
In many ways, this disconnect between biological neurons and artificial neurons is quite unfortunate. Uninitiated experts read breathless press releases claiming artificial neural networks with billions of “neurons” have been created (while the brain has only 100 billion biological neurons) and reasonably come away believing scientists are close to creating human-level intelligences. Needless to say, state of the art in deep learning is decades (or centuries) away from such an achievement.
As you read further about deep learning, you may come across overhyped claims about artificial intelligence. Don’t be afraid to call out these statements. Deep learning in its current form is a set of techniques for solving calculus problems on fast hardware. It is not a precursor to Terminator (Figure 4-4).

Figure 4-4. Unfortunately (or perhaps fortunately), this book won’t teach you to build a Terminator!
AI Winters
Artificial intelligence has gone through multiple rounds of boom-and-bust development. This cyclical development is characteristic of the field. Each new advance in learning spawns a wave of optimism in which prophets claim that human-level (or superhuman) intelligences are incipient. After a few years, no such intelligences manifest, and disappointed funders pull out. The resulting period is called an AI winter.
There have been multiple AI winters so far. As a thought exercise, we encourage you to consider when the next AI winter will happen. The current wave of deep learning progress has solved many more practical problems than any previous wave of advances. Is it possible AI has finally taken off and exited the boom-and-bust cycle or do you think we’re in for the “Great Depression” of AI soon?
Learning Fully Connected Networks with Backpropagation
The first version of a fully connected neural network was the Perceptron, (Figure 4-5), created by Frank Rosenblatt in the 1950s. These perceptrons are identical to the “neurons” we introduced in the previous equations.
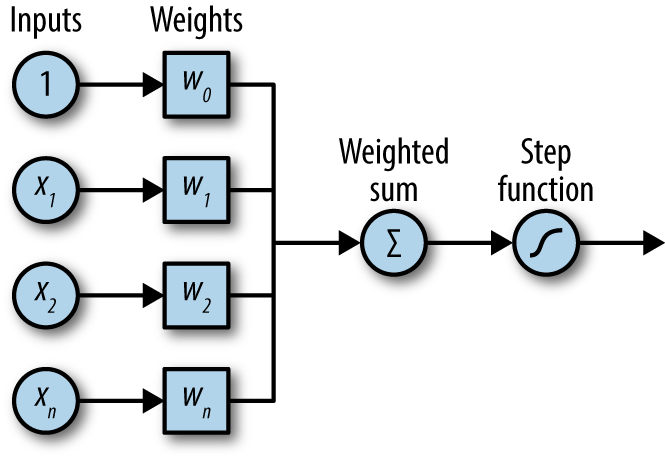
Figure 4-5. A diagrammatic representation of the perceptron.
Perceptrons were trained by a custom “perceptron” rule. While they were moderately useful solving simple problems, perceptrons were fundamentally limited. The book Perceptrons by Marvin Minsky and Seymour Papert from the end of the 1960s proved that simple perceptrons were incapable of learning the XOR function. Figure 4-6 illustrates the proof of this statement.
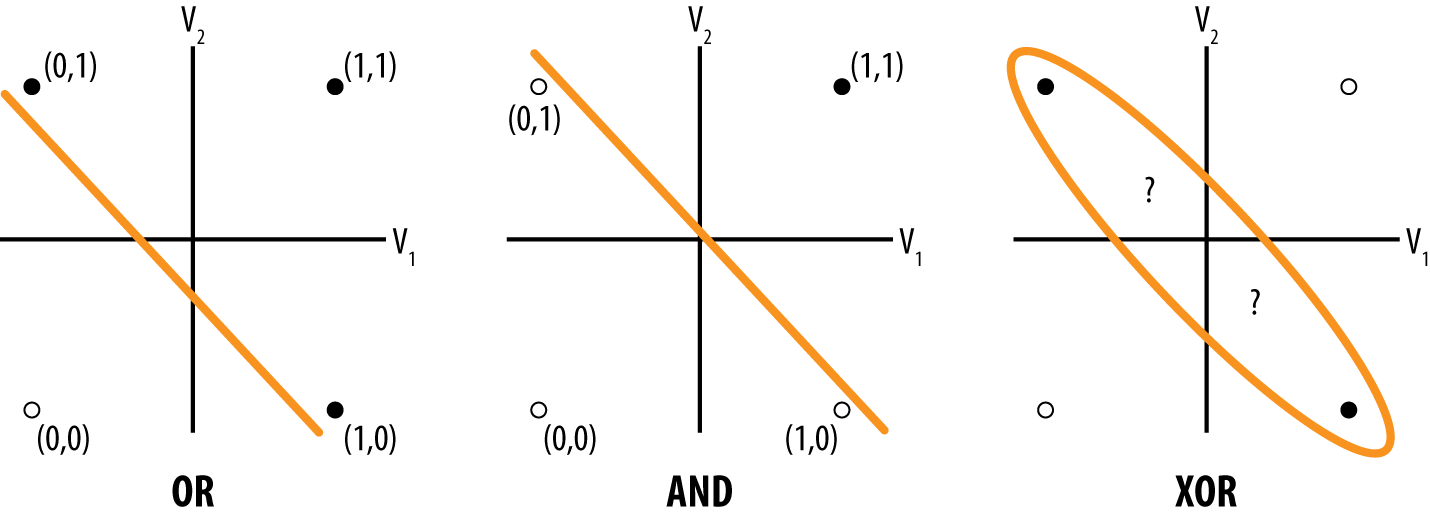
Figure 4-6. The perceptron’s linear rule can’t learn the perceptron.
This problem was overcome with the invention of the multilayer perceptron (another name for a deep fully connected network). This invention was a formidable achievement, since earlier simple learning algorithms couldn’t learn deep networks effectively. The “credit assignment” problem stumped them; how does an algorithm decide which neuron learns what?
The full solution to this problem requires backpropagation. Backpropagation is a generalized rule for learning the weights of neural networks. Unfortunately, complicated explanations of backpropagation are epidemic in the literature. This situation is unfortunate since backpropagation is simply another word for automatic differentiation.
Let’s suppose that is a function that represents a deep fully connected network. Here is the inputs to the fully connected network and is the learnable weights. Then the backpropagation algorithm simply computes . The practical complexities arise in implementing backpropagation for all possible functions f that arise in practice. Luckily for us, TensorFlow takes care of this already!
Universal Convergence Theorem
The preceding discussion has touched on the ideas that deep fully connected networks are powerful approximations. McCulloch and Pitts showed that logical networks can code (almost) any Boolean function. Rosenblatt’s Perceptron was the continuous analog of McCulloch and Pitt’s logical functions, but was shown to be fundamentally limited by Minsky and Papert. Multilayer perceptrons looked to solve the limitations of simple perceptrons and empirically seemed capable of learning complex functions. However, it wasn’t theoretically clear whether this empirical ability had undiscovered limitations. In 1989, George Cybenko demonstrated that multilayer perceptrons were capable of representing arbitrary functions. This demonstration provided a considerable boost to the claims of generality for fully connected networks as a learning architecture, partially explaining their continued popularity.
However, if both backpropagation and fully connected network theory were understood in the late 1980s, why didn’t “deep” learning become more popular earlier? A large part of this failure was due to computational limitations; learning fully connected networks took an exorbitant amount of computing power. In addition, deep networks were very difficult to train due to lack of understanding about good hyperparameters. As a result, alternative learning algorithms such as SVMs that had lower computational requirements became more popular. The recent surge in popularity in deep learning is partly due to the increased availability of better computing hardware that enables faster computing, and partly due to increased understanding of good training regimens that enable stable learning.
Is Universal Approximation That Surprising?
Universal approximation properties are more common in mathematics than one might expect. For example, the Stone-Weierstrass theorem proves that any continuous function on a closed interval can be a suitable polynomial function. Loosening our criteria further, Taylor series and Fourier series themselves offer some universal approximation capabilities (within their domains of convergence). The fact that universal convergence is fairly common in mathematics provides partial justification for the empirical observation that there are many slight variants of fully connected networks that seem to share a universal approximation property.
Universal Approximation Doesn’t Mean Universal Learning!
A critical subtlety exists in the universal approximation theorem. The fact that a fully connected network can represent any function doesn’t mean that backpropagation can learn any function! One of the major limitations of backpropagation is that there is no guarantee the fully connected network “converges”; that is, finds the best available solution of a learning problem. This critical theoretical gap has left generations of computer scientists queasy with neural networks. Even today, many academics will prefer to work with alternative algorithms that have stronger theoretical guarantees.
Empirical research has yielded many practical tricks that allow backpropagation to find good solutions for problems. We will go into many of these tricks in significant depth in the remainder of this chapter. For the practicing data scientist, the universal approximation theorem isn’t something to take too seriously. It’s reassuring, but the art of deep learning lies in mastering the practical hacks that make learning work.
Why Deep Networks?
A subtlety in the universal approximation theorem is that it in fact holds true for fully connected networks with only one fully connected layer. What then is the use of “deep” learning with multiple fully connected layers? It turns out that this question is still quite controversial in academic and practical circles.
In practice, it seems that deeper networks can sometimes learn richer models on large datasets. (This is only a rule of thumb, however; every practitioner has a bevy of examples where deep fully connected networks don’t do well.) This observation has led researchers to hypothesize that deeper networks can represent complex functions “more efficiently.” That is, a deeper network may be able to learn more complex functions than shallower networks with the same number of neurons. For example, the ResNet architecture mentioned briefly in the first chapter, with 130 layers, seems to outperform its shallower competitors such as AlexNet. In general, for a fixed neuron budget, stacking deeper leads to better results.
A number of erroneous “proofs” for this “fact” have been given in the literature, but all of them have holes. It seems the question of depth versus width touches on profound concepts in complexity theory (which studies the minimal amount of resources required to solve given computational problems). At present day, it looks like theoretically demonstrating (or disproving) the superiority of deep networks is far outside the ability of our mathematicians.
Training Fully Connected Neural Networks
As we mentioned previously, the theory of fully connected networks falls short of practice. In this section, we will introduce you to a number of empirical observations about fully connected networks that aid practitioners. We strongly encourage you to use our code (introduced later in the chapter) to check our claims for yourself.
Learnable Representations
One way of thinking about fully connected networks is that each fully connected layer effects a transformation of the feature space in which the problem resides. The idea of transforming the representation of a problem to render it more malleable is a very old one in engineering and physics. It follows that deep learning methods are sometimes called “representation learning.” (An interesting factoid is that one of the major conferences for deep learning is called the “International Conference on Learning Representations.”)
Generations of analysts have used Fourier transforms, Legendre transforms, Laplace transforms, and so on in order to simplify complicated equations and functions to forms more suitable for handwritten analysis. One way of thinking about deep learning networks is that they effect a data-driven transform suited to the problem at hand.
The ability to perform problem-specific transformations can be immensely powerful. Standard transformation techniques couldn’t solve problems of image or speech analysis, while deep networks are capable of solving these problems with relative ease due to the inherent flexibility of the learned representations. This flexibility comes with a price: the transformations learned by deep architectures tend to be much less general than mathematical transforms such as the Fourier transform. Nonetheless, having deep transforms in an analytic toolkit can be a powerful problem-solving tool.
There’s a reasonable argument that deep learning is simply the first representation learning method that works. In the future, there may well be alternative representation learning methods that supplant deep learning methods.
Activations
We previously introduced the nonlinear function as the sigmoidal function. While the sigmoidal is the classical nonlinearity in fully connected networks, in recent years researchers have found that other activations, notably the rectified linear activation (commonly abbreviated ReLU or relu) work better than the sigmoidal unit. This empirical observation may be due to the vanishing gradient problem in deep networks. For the sigmoidal function, the slope is zero for almost all values of its input. As a result, for deeper networks, the gradient would tend to zero. For the ReLU function, the slope is nonzero for a much greater part of input space, allowing nonzero gradients to propagate. Figure 4-7 illustrates sigmoidal and ReLU activations side by side.
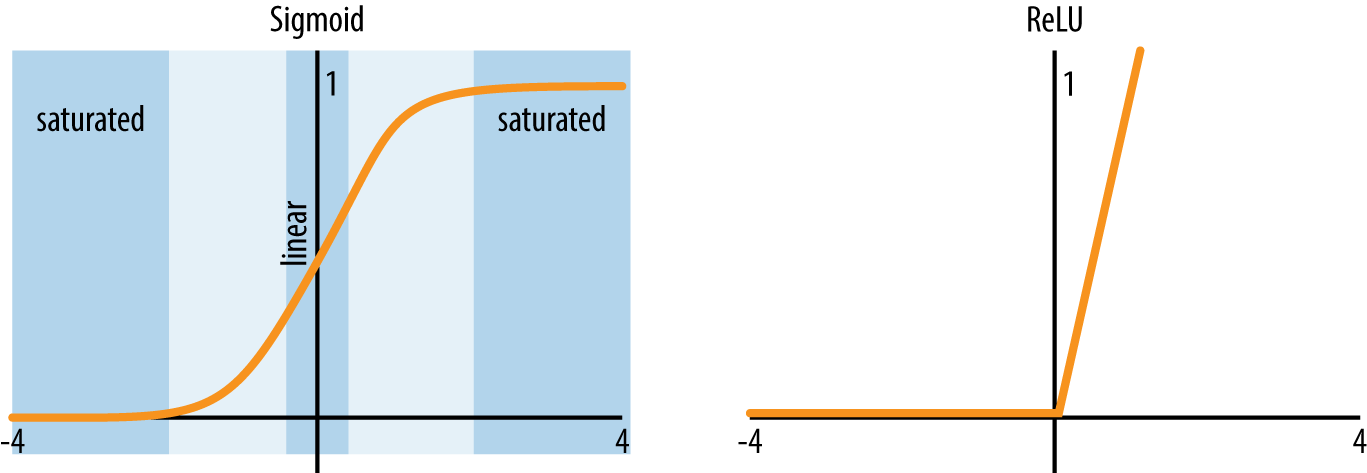
Figure 4-7. Sigmoidal and ReLU activation functions.
Fully Connected Networks Memorize
One of the striking aspects about fully connected networks is that they tend to memorize training data entirely given enough time. As a result, training a fully connected network to “convergence” isn’t really a meaningful metric. The network will keep training and learning as long as the user is willing to wait.
For large enough networks, it is quite common for training loss to trend all the way to zero. This empirical observation is one the most practical demonstrations of the universal approximation capabilities of fully connected networks. Note however, that training loss trending to zero does not mean that the network has learned a more powerful model. It’s rather likely that the model has started to memorize peculiarities of the training set that aren’t applicable to any other datapoints.
It’s worth digging into what we mean by peculiarities here. One of the interesting properties of high-dimensional statistics is that given a large enough dataset, there will be plenty of spurious correlations and patterns available for the picking. In practice, fully connected networks are entirely capable of finding and utilizing these spurious correlations. Controlling networks and preventing them from misbehaving in this fashion is critical for modeling success.
Regularization
Regularization is the general statistical term for a mathematical operation that limits memorization while promoting generalizable learning. There are many different types of regularization available, which we will cover in the next few sections.
Not Your Statistician’s Regularization
Regularization has a long history in the statistical literature, with entire sheaves of papers written on the topic. Unfortunately, only some of this classical analysis carries over to deep networks. The linear models used widely in statistics can behave very differently from deep networks, and many of the intuitions built in that setting can be downright wrong for deep networks.
The first rule for working with deep networks, especially for readers with prior statistical modeling experience, is to trust empirical results over past intuition. Don’t assume that past knowledge about techniques such as LASSO has much meaning for modeling deep architectures. Rather, set up an experiment to methodically test your proposed idea. We will return at greater depth to this methodical experimentation process in the next chapter.
Dropout
Dropout is a form of regularization that randomly drops some proportion of the nodes that feed into a fully connected layer (Figure 4-8). Here, dropping a node means that its contribution to the corresponding activation function is set to 0. Since there is no activation contribution, the gradients for dropped nodes drop to zero as well.
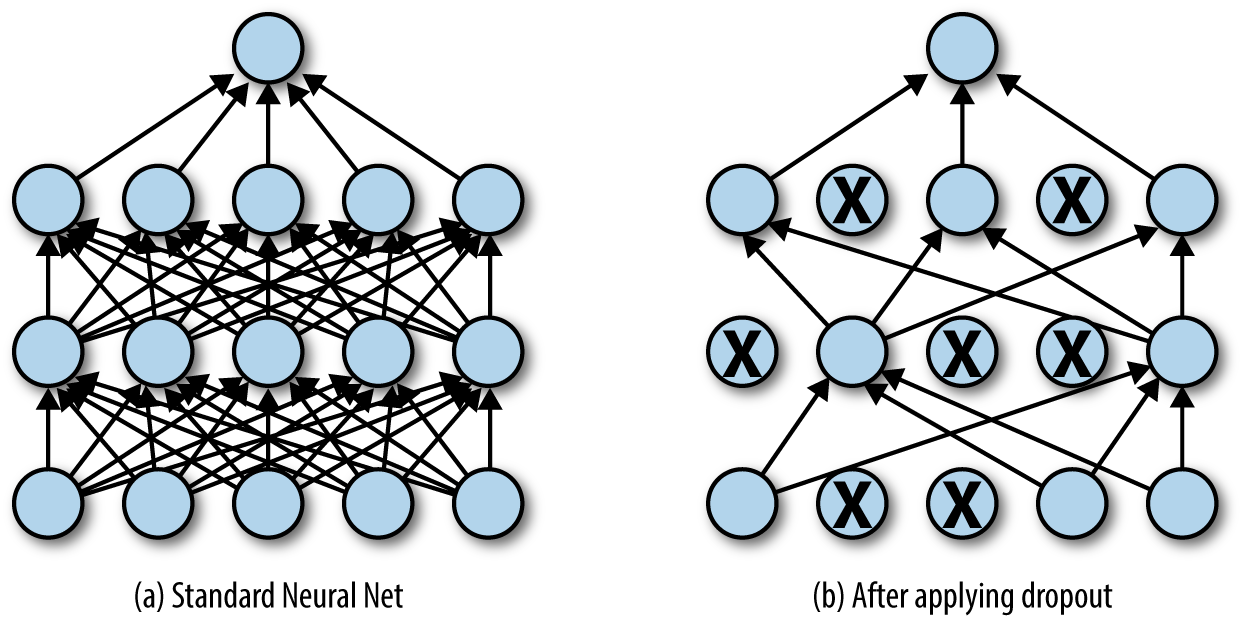
Figure 4-8. Dropout randomly drops neurons from a network while training. Empirically, this technique often provides powerful regularization for network training.
The nodes to be dropped are chosen at random during each step of gradient descent. The underlying design principle is that the network will be forced to avoid “co-adaptation.” Briefly, we will explain what co-adaptation is and how it arises in non-regularized deep architectures. Suppose that one neuron in a deep network has learned a useful representation. Then other neurons deeper in the network will rapidly learn to depend on that particular neuron for information. This process will render the network brittle since the network will depend excessively on the features learned by that neuron, which might represent a quirk of the dataset, instead of learning a general rule.
Dropout prevents this type of co-adaptation because it will no longer be possible to depend on the presence of single powerful neurons (since that neuron might drop randomly during training). As a result, other neurons will be forced to “pick up the slack” and learn useful representations as well. The theoretical argument follows that this process should result in stronger learned models.
In practice, dropout has a pair of empirical effects. First, it prevents the network from memorizing the training data; with dropout, training loss will no longer tend rapidly toward 0, even for very large deep networks. Next, dropout tends to slightly boost the predictive power of the model on new data. This effect often holds for a wide range of datasets, part of the reason that dropout is recognized as a powerful invention, and not just a simple statistical hack.
You should note that dropout should be turned off when making predictions. Forgetting to turn off dropout can cause predictions to be much noisier and less useful than they would be otherwise. We discuss how to handle dropout for training and predictions correctly later in the chapter.
How Can Big Networks Not Overfit?
One of the most jarring points for classically trained statisticians is that deep networks may routinely have more internal degrees of freedom than are present in the training data. In classical statistics, the presence of these extra degrees of freedom would render the model useless, since there will no longer exist a guarantee that the model learned is “real” in the classical sense.
How then can a deep network with millions of parameters learn meaningful results on datasets with only thousands of exemplars? Dropout can make a big difference here and prevent brute memorization. But, there’s also a deeper unexplained mystery in that deep networks will tend to learn useful facts even in the absence of dropout. This tendency might be due to some quirk of backpropagation or fully connected network structure that we don’t yet understand.
Early stopping
As mentioned, fully connected networks tend to memorize whatever is put before them. As a result, it’s often useful in practice to track the performance of the network on a held-out “validation” set and stop the network when performance on this validation set starts to go down. This simple technique is known as early stopping.
In practice, early stopping can be quite tricky to implement. As you will see, loss curves for deep networks can vary quite a bit in the course of normal training. Devising a rule that separates healthy variation from a marked downward trend can take significant effort. In practice, many practitioners just train models with differing (fixed) numbers of epochs, and choose the model that does best on the validation set. Figure 4-9 illustrates how training and test set accuracy typically change as training proceeds.
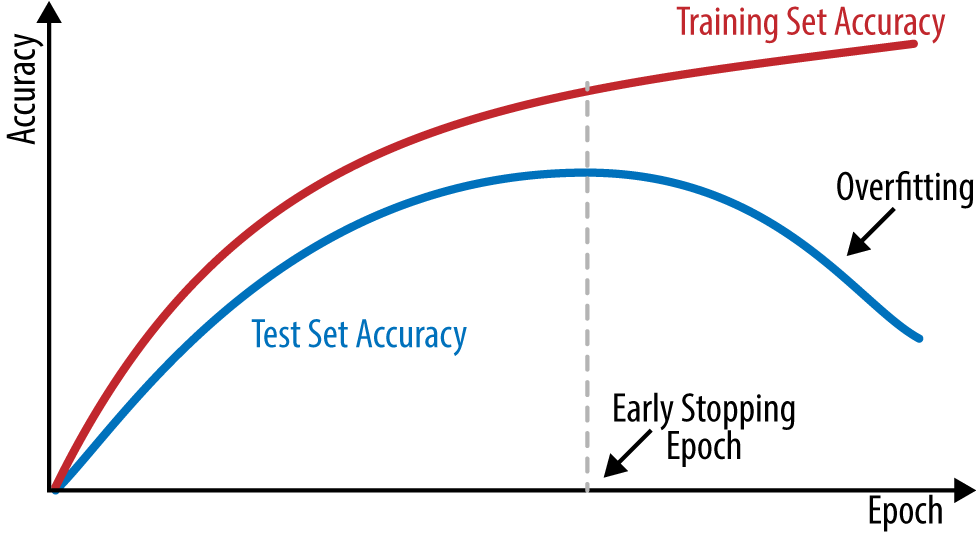
Figure 4-9. Model accuracy on training and test sets as training proceeds.
We will dig more into proper methods for working with validation sets in the following chapter.
Weight regularization
A classical regularization technique drawn from the statistical literature penalizes learned weights that grow large. Following notation from the previous chapter, let denote the loss function for a particular model and let denote the learnable parameters of this model. Then the regularized loss function is defined by
where is the weight penalty and is a tunable parameter. The two common choices for penalty are the L1 and L2 penalties
where and denote the L1 and L2 penalties, respectively. From personal experience, these penalties tend to be less useful for deep models than dropout and early stopping. Some practitioners still make use of weight regularization, so it’s worth understanding how to apply these penalties when tuning deep networks.
Training Fully Connected Networks
Training fully connected networks requires a few tricks beyond those you have seen so far in this book. First, unlike in the previous chapters, we will train models on larger datasets. For these datasets, we will show you how to use minibatches to speed up gradient descent. Second, we will return to the topic of tuning learning rates.
Minibatching
For large datasets (which may not even fit in memory), it isn’t feasible to compute gradients on the full dataset at each step. Rather, practitioners often select a small chunk of data (typically 50–500 datapoints) and compute the gradient on these datapoints. This small chunk of data is traditionally called a minibatch.
In practice, minibatching seems to help convergence since more gradient descent steps can be taken with the same amount of compute. The correct size for a minibatch is an empirical question often set with hyperparameter tuning.
Learning rates
The learning rate dictates the amount of importance to give to each gradient descent step. Setting a correct learning rate can be tricky. Many beginning deep-learners set learning rates incorrectly and are surprised to find that their models don’t learn or start returning NaNs. This situation has improved significantly with the development of methods such as ADAM that simplify choice of learning rate significantly, but it’s worth tweaking the learning rate if models aren’t learning anything.
Implementation in TensorFlow
In this section, we will show you how to implement a fully connected network in TensorFlow. We won’t need to introduce many new TensorFlow primitives in this section since we have already covered most of the required basics.
Installing DeepChem
In this section, you will use the DeepChem machine learning toolchain for your experiments (full disclosure: one of the authors was the creator of DeepChem). Detailed installation directions for DeepChem can be found online, but briefly the Anaconda installation via the conda tool will likely be most convenient.
Tox21 Dataset
For our modeling case study, we will use a chemical dataset. Toxicologists are very interested in the task of using machine learning to predict whether a given compound will be toxic or not. This task is extremely complicated, since today’s science has only a limited understanding of the metabolic processes that happen in a human body. However, biologists and chemists have worked out a limited set of experiments that provide indications of toxicity. If a compound is a “hit” in one of these experiments, it will likely be toxic for a human to ingest. However, these experiments are often costly to run, so data scientists aim to build machine learning models that can predict the outcomes of these experiments on new molecules.
One of the most important toxicological dataset collections is called Tox21. It was released by the NIH and EPA as part of a data science initiative and was used as the dataset in a model building challenge. The winner of this challenge used multitask fully connected networks (a variant of fully connected networks where each network predicts multiple quantities for each datapoint). We will analyze one of the datasets from the Tox21 collection. This dataset consists of a set of 10,000 molecules tested for interaction with the androgen receptor. The data science challenge is to predict whether new molecules will interact with the androgen receptor.
Processing this dataset can be tricky, so we will make use of the MoleculeNet dataset collection curated as part of DeepChem. Each molecule in Tox21 is processed into a bit-vector of length 1024 by DeepChem. Loading the dataset is then a few simple calls into DeepChem (Example 4-1).
Example 4-1. Load the Tox21 dataset
importdeepchemasdc_,(train,valid,test),_=dc.molnet.load_tox21()train_X,train_y,train_w=train.X,train.y,train.wvalid_X,valid_y,valid_w=valid.X,valid.y,valid.wtest_X,test_y,test_w=test.X,test.y,test.w
Here the X variables hold processed feature vectors, y holds labels, and w holds example weights. The labels are binary 1/0 for compounds that interact or don’t interact with the androgen receptor. Tox21 holds imbalanced datasets, where there are far fewer positive examples than negative examples. w holds recommended per-example weights that give more emphasis to positive examples (increasing the importance of rare examples is a common technique for handling imbalanced datasets). We won’t use these weights during training for simplicity. All of these variables are NumPy arrays.
Tox21 has more datasets than we will analyze here, so we need to remove the labels associated with these extra datasets (Example 4-2).
Example 4-2. Remove extra datasets from Tox21
# Remove extra taskstrain_y=train_y[:,0]valid_y=valid_y[:,0]test_y=test_y[:,0]train_w=train_w[:,0]valid_w=valid_w[:,0]test_w=test_w[:,0]
Accepting Minibatches of Placeholders
In the previous chapters, we created placeholders that accepted arguments of fixed size. When dealing with minibatched data, it is often convenient to be able to feed batches of variable size. Suppose that a dataset has 947 elements. Then with a minibatch size of 50, the last batch will have 47 elements. This would cause the code in Chapter 3 to crash. Luckily, TensorFlow has a simple fix to the situation: using None as a dimensional argument to a placeholder allows the placeholder to accept tensors with arbitrary size in that dimension (Example 4-3).
Example 4-3. Defining placeholders that accept minibatches of different sizes
d=1024withtf.name_scope("placeholders"):x=tf.placeholder(tf.float32,(None,d))y=tf.placeholder(tf.float32,(None,))
Note d is 1024, the dimensionality of our feature vectors.
Implementing a Hidden Layer
The code to implement a hidden layer is very similar to code we’ve seen in the last chapter for implementing logistic regression, as shown in Example 4-4.
We use a tf.name_scope to group together introduced variables. Note that we use the matricial form of the fully connected layer. We use the form xW instead of Wx in order to deal more conveniently with a minibatch of input at a time. (As an exercise, try working out the dimensions involved to see why this is so.) Finally, we apply the ReLU nonlinearity with the built-in tf.nn.relu activation function.
The remainder of the code for the fully connected layer is quite similar to that used for the logistic regression in the previous chapter. For completeness, we display the full code used to specify the network in Example 4-5. As a quick reminder, the full code for all models covered is available in the GitHub repo associated with this book. We strongly encourage you to try running the code for yourself.
Example 4-5. Defining the fully connected architecture
withtf.name_scope("placeholders"):x=tf.placeholder(tf.float32,(None,d))y=tf.placeholder(tf.float32,(None,))withtf.name_scope("hidden-layer"):W=tf.Variable(tf.random_normal((d,n_hidden)))b=tf.Variable(tf.random_normal((n_hidden,)))x_hidden=tf.nn.relu(tf.matmul(x,W)+b)withtf.name_scope("output"):W=tf.Variable(tf.random_normal((n_hidden,1)))b=tf.Variable(tf.random_normal((1,)))y_logit=tf.matmul(x_hidden,W)+b# the sigmoid gives the class probability of 1y_one_prob=tf.sigmoid(y_logit)# Rounding P(y=1) will give the correct prediction.y_pred=tf.round(y_one_prob)withtf.name_scope("loss"):# Compute the cross-entropy term for each datapointy_expand=tf.expand_dims(y,1)entropy=tf.nn.sigmoid_cross_entropy_with_logits(logits=y_logit,labels=y_expand)# Sum all contributionsl=tf.reduce_sum(entropy)withtf.name_scope("optim"):train_op=tf.train.AdamOptimizer(learning_rate).minimize(l)withtf.name_scope("summaries"):tf.summary.scalar("loss",l)merged=tf.summary.merge_all()
Adding Dropout to a Hidden Layer
TensorFlow takes care of implementing dropout for us in the built-in primitive tf.nn.dropout(x, keep_prob), where keep_prob is the probability that any given node is kept. Recall from our earlier discussion that we want to turn on dropout when training and turn off dropout when making predictions. To handle this correctly, we will introduce a new placeholder for keep_prob, as shown in Example 4-6.
Example 4-6. Add a placeholder for dropout probability
keep_prob=tf.placeholder(tf.float32)
During training, we pass in the desired value, often 0.5, but at test time we set keep_prob to 1.0 since we want predictions made with all learned nodes. With this setup, adding dropout to the fully connected network specified in the previous section is simply a single extra line of code (Example 4-7).
Implementing Minibatching
To implement minibatching, we need to pull out a minibatch’s worth of data each time we call sess.run. Luckily for us, our features and labels are already in NumPy arrays, and we can make use of NumPy’s convenient syntax for slicing portions of arrays (Example 4-8).
Example 4-8. Training on minibatches
step=0forepochinrange(n_epochs):pos=0whilepos<N:batch_X=train_X[pos:pos+batch_size]batch_y=train_y[pos:pos+batch_size]feed_dict={x:batch_X,y:batch_y,keep_prob:dropout_prob}_,summary,loss=sess.run([train_op,merged,l],feed_dict=feed_dict)("epoch%d, step%d, loss:%f"%(epoch,step,loss))train_writer.add_summary(summary,step)step+=1pos+=batch_size
Evaluating Model Accuracy
To evaluate model accuracy, standard practice requires measuring the accuracy of the model on data not used for training (namely the validation set). However, the fact that the data is imbalanced makes this tricky. The classification accuracy metric we used in the previous chapter simply measures the fraction of datapoints that were labeled correctly. However, 95% of data in our dataset is labeled 0 and only 5% are labeled 1. As a result the all-0 model (which labels everything negative) would achieve 95% accuracy! This isn’t what we want.
A better choice would be to increase the weights of positive examples so that they count for more. For this purpose, we use the recommended per-example weights from MoleculeNet to compute a weighted classification accuracy where positive samples are weighted 19 times the weight of negative samples. Under this weighted accuracy, the all-0 model would have 50% accuracy, which seems much more reasonable.
For computing the weighted accuracy, we use the function accuracy_score(true, pred, sample_weight=given_sample_weight) from sklearn.metrics. This function has a keyword argument sample_weight, which lets us specify the desired weight for each datapoint. We use this function to compute the weighted metric on both the training and validation sets (Example 4-9).
Example 4-9. Computing a weighted accuracy
train_weighted_score=accuracy_score(train_y,train_y_pred,sample_weight=train_w)("Train Weighted Classification Accuracy:%f"%train_weighted_score)valid_weighted_score=accuracy_score(valid_y,valid_y_pred,sample_weight=valid_w)("Valid Weighted Classification Accuracy:%f"%valid_weighted_score)
While we could reimplement this function ourselves, sometimes it’s easier (and less error prone) to use standard functions from the Python data science infrastructure. Learning about this infrastructure and available functions is part of being a practicing data scientist. Now, we can train the model (for 10 epochs in the default setting) and gauge its accuracy:
Train Weighted Classification Accuracy: 0.742045 Valid Weighted Classification Accuracy: 0.648828
In Chapter 5, we will show you methods to systematically improve this accuracy and tune our fully connected model more carefully.
Using TensorBoard to Track Model Convergence
Now that we have specified our model, let’s use TensorBoard to inspect the model. Let’s first check the graph structure in TensorBoard (Figure 4-10).
The graph looks similar to that for logistic regression, with the addition of a new hidden layer. Let’s expand the hidden layer to see what’s inside (Figure 4-11).
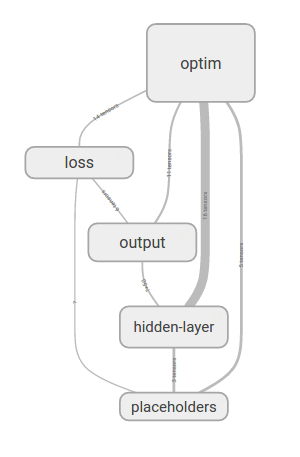
Figure 4-10. Visualizing the computation graph for a fully connected network.
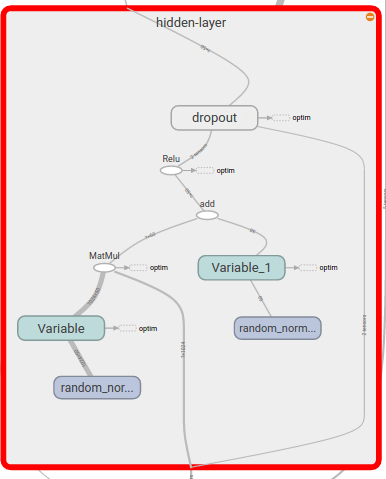
Figure 4-11. Visualizing the expanded computation graph for a fully connected network.
You can see how the new trainable variables and the dropout operation are represented here. Everything looks to be in the right place. Let’s end now by looking at the loss curve over time (Figure 4-12).
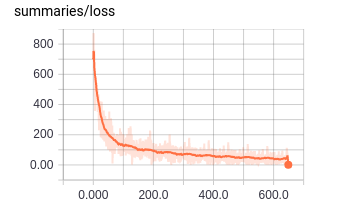
Figure 4-12. Visualizing the loss curve for a fully connected network.
The loss curve trends down as we saw in the previous section. But, let’s zoom in to see what this loss looks like up close (Figure 4-13).
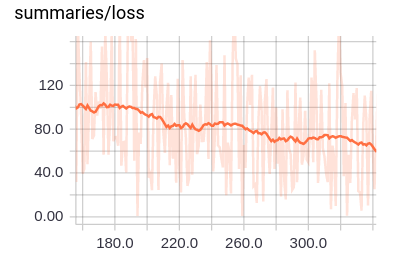
Figure 4-13. Zooming in on a section of the loss curve.
Note that loss looks much bumpier! This is one of the prices of using minibatch training. We no longer have the beautiful, smooth loss curves that we saw in the previous sections.
Review
In this chapter, we’ve introduced you to fully connected deep networks. We delved into the mathematical theory of these networks, and explored the concept of “universal approximation,” which partially explains the learning power of fully connected networks. We ended with a case study, where you trained a deep fully connected architecture on the Tox21 dataset.
In this chapter, we haven’t yet shown you how to tune the fully connected network to achieve good predictive performance. In Chapter 5, we will discuss “hyperparameter optimization,” the process of tuning network parameters, and have you tune the parameters of the Tox21 network introduced in this chapter.
Get TensorFlow for Deep Learning now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

