Appendices
A.1 Hamming Code
Hamming code ([89] in Chapter 7) is the most commonly used in computer applications. For given integer m, code length n is given by n = 2m − 1, while data length is given by k = n − m in Hamming code.
Typically, a check matrix H and a generator matrix G are utilized and should be defined in Hamming Code to detect and correct a data vector.
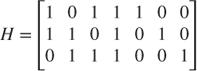
Generator matrix G is given from H as,
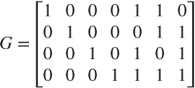
All column vector in matrices H and G must be independent and must not be null vector (all elements are ‘0’s).
When the data bits are x = [1 1 0 1], the codeword can be calculated by multiplying x and G,
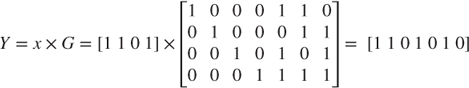
It is noteworthy that all additional calculations are exclusive or (XOR) in this matrix calculation.
If Y is correctly converted,
If not, the result of the above calculation, syndrome, gives the same vector as the one of the column vectors of the check matrix H where one bit error is introduced. When two-bit errors take place, the calculated results indicate the wrong column vector. In that case, the following check matrix in the extended Hamming code is utilised, ...
Get Terrestrial Radiation Effects in ULSI Devices and Electronic Systems now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

