Appendix B
Generalized Gauss Laguerre Quadrature
We outline two algorithms for the computation of abscissas and weights for generalized Gauss Laguerre quadrature.
B.1 EIGENVALUE PROBLEM
The first algorithm is based on an eigenvalue problem. We refer to Golub and Welsch (1969) and Wilf (1962) for a detailed discussion. The abscissas of the quadrature formula can be found as the eigenvalues of the symmetric tridiagonal matrix T, given by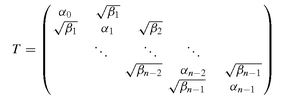 where αi = 2i + 1 + s and βi = i(i + s). The corresponding weights can be computed from the normalized eigenvectors. With
where αi = 2i + 1 + s and βi = i(i + s). The corresponding weights can be computed from the normalized eigenvectors. With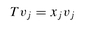 where = 1 we have that
where = 1 we have that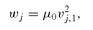 where µ0 = w(x ;s) = ┌(s + 1) .
where µ0 = w(x ;s) = ┌(s + 1) .
(B.1)
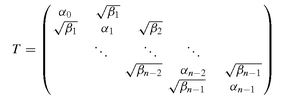
(B.2)
(B.3)
The symmetric tridiagonal eigenvalue problem as in (B.2) can be solved efficiently using the classical algorithms for eigenvalues; see Golub and Van Loan (1989), Parlett (1980) or Wilkinson (1988) for details. This and other numerical algorithms are addressed in Press et al. (1992). Note that only the first component of the normalized eigenvector is required, hence an optimized eigenvalue solver can be used.
B.2 NEWTON-RAPHSON ITERATION
The second algorithm is based on the fact that good initial approximations for the zeros of the orthogonal polynomials are ...
Get The Art of Credit Derivatives: Demystifying the Black Swan now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

