The Handbook of News Analytics in Finance

13.2 MODEL DESCRIPTION

The model provides updated estimates of portfolio volatility using information about changes to the market environment. We describe in this section a slightly modified form of the model outlined in diBartolomeo and Warrick (2005) which updates traditional factor risk estimates using option-implied volatility. This model is extended in the following section with quantified news inputs.

The model is described in two parts. The first is a “basic” statistical factor model. In the second part, factor variance estimates are updated to account for changes in option-implied volatility levels. The asset covariance matrix is re-estimated, using the updated factor variances, to give an improved set of risk estimates.

We construct a statistical factor model applying traditional principal component analysis to extract orthogonal factors.¹ For a general factor model, the variance of each asset is given as a linear combination of factor variances and asset-specific variances

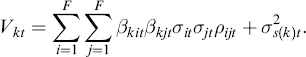
Sets and indices

k ∈ {1, …, N₁} denotes the asset universe;

t ∈ {1, …, T} denotes the time points considered;

i, j ∈ {1, …, F} denotes the factors.

Parameters

Vkt	denotes the variance for asset k at time point t ∈ {1,…, T};
βkit	denotes factor sensitivity (exposure) to factor i for asset k at time point t;
σit	denotes factor variance for factor i at time point t;
ρijt	denotes the correlation ...