
The Heston Model for European Options
Abstract
In this chapter, we present a complete derivation of the European call price under the Heston model. We first present the model and obtain the various partial differential equations (PDEs) that arise in the derivation. We show that the call price in the Heston model can be expressed as the sum of two terms that each contains an in-he-money probability, but obtained under a separate measure, a result demonstrated by Bakshi and Madan (2000). We show how to obtain the characteristic function for the Heston model, and how to solve the Riccati equation from which the characteristic function is derived. We then show how to incorporate a continuous dividend yield and how to compute the price of a European put, and demonstrate that the numerical integration can be speeded up by consolidating the two numerical integrals into a single integral. Finally, we derive the Black-Scholes model as a special case of the Heston model.
MODEL DYNAMICS
The Heston model assumes that the underlying stock price, St, follows a Black-Scholes-type stochastic process, but with a stochastic variance vt that follows a Cox, Ingersoll, and Ross (1985) process. Hence, the Heston model is represented by the bivariate system of stochastic differential equations (SDEs)
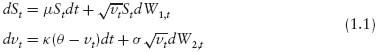
Get The Heston Model and its Extensions in Matlab and C#, + Website now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

