The Mathematics of Derivatives: Tools for Designing Numerical Algorithms

CHAPTER 3

Stochastic Calculus

3.1. WIENER PROCESS

We have already looked at the concept of a random walk, starting at zero,

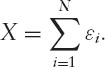
The result of N steps of size 1 in a randomly selected direction gets the walker to position X; the mean of X is zero and the standard deviation of X is in the large N limit. The same is true for any shock of the same standard deviation and mean, for example, if each ε_i is selected from a normal distribution of standard deviation 1 and mean 0.

In this chapter, we modify the analysis slightly. We will make the steps occur every increment of time Δt, and the step is going to be selected from a random distribution of mean zero and standard deviation ,

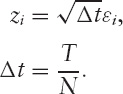
Then define

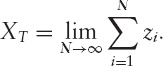
This formula is mathematically well defined for any finite N; because the behavior is smooth over large values of N, the limit for N → ∞, is well-defined as well. Visually we have a wiggly path. But it is impossible to correctly draw! This is because it has a fractal nature to it. No matter how small you ...