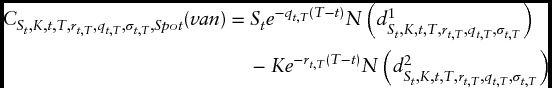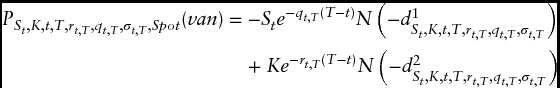The Mathematics of Financial Models: Solving Real-World Problems with Quantitative Methods

CHAPTER 6 Estimating Model Parameters

In Chapters 3, 4, and 5, I discussed the valuation of options when the variability entered only through future price (value or rate) movements. As a consequence, the bulk of my discussion in this chapter will focus on the estimation of model parameters when there is only price stochasticity. As in Chapter 5, I will continue to assume that the underlying is an index that pays continuous dividends.

I showed in Chapter 3 how equations (3.7a) and (3.7b)—were used to value European-style options on a stock that pays a continuously compounded dividend. For the ease of reading, I have re-stated these equations again:

(3.7a)

(3.7b)

where

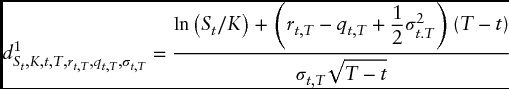
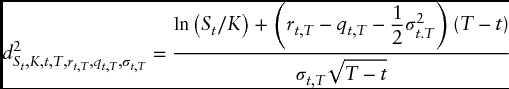
When illustrating the implementation of equations (3.7a) and (3.7b) in Table 3.4, I assumed that all the inputs going into the model (e.g., S_t, K, t, T, r_{t, T}, q_{t, T}, σ_{t, T}) are known—which is far from the truth in practice. In reality, the only inputs that are known with 100 percent objectivity are S_t, K, t, T. In fact, while S_t represents the value of the observable index at the time of valuation, the ...