The R Book

Robust Fitting of Linear Models

This uses the rlm function from the MASS library. The function allows one to fit a linear model by robust regression using an M estimator, allowing robust inference for parameters and robust model selection. The robust fit is minimally influenced by outliers in the response variable, in the explanatory variable(s) or in both.

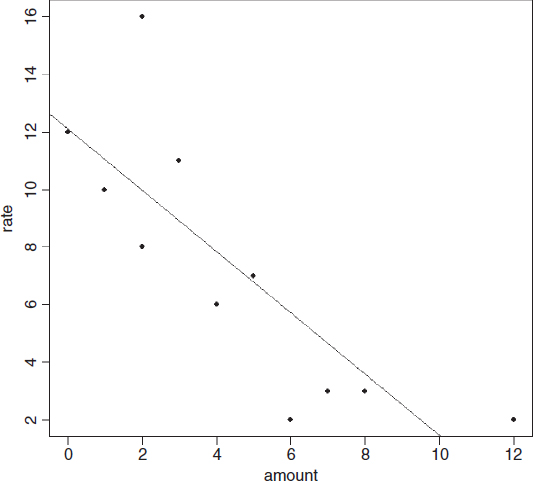
robreg<-read.table("c:\\temp\\robreg.txt",header=T)
attach(robreg)
names(robreg)

[1] "amount" "rate"

plot(amount,rate,pch=16)
abline(lm(rate~amount))
summary(lm(rate~amount))

Coefficients:
             Estimate Std. Error t value   Pr(>|t|)
(Intercept)   12.1064     1.4439   8.385   1.52e-05  ***
     amount   -1.0634     0.2552  -4.166    0.00243   **

Residual standard error: 2.851 on 9 degrees of freedom
Multiple R-Squared: 0.6585, Adjusted R-squared: 0.6206
F-statistic: 17.36 on 1 and 9 DF, p-value: 0.002425

We can leave out the maximum and minimum values of the response or explanatory variables separately or together using subset to test for influence:

summary(lm(rate~amount,subset=(rate<max(rate))))

Coefficients:

              Estimate   Std. Error   t value   Pr(>|t|)
(Intercept)    10.8163       1.0682    10.126   7.73e-06 ***
amount         -0.9201       0.1811    -5.081   0.000952 ***

Residual standard error: 1.964 on 8 degrees of freedom
Multiple R-Squared: 0.7634, Adjusted R-squared: 0.7339
F-statistic: 25.82 on 1 and 8 DF, p-value: 0.000952

The intercept is lower by more than 1.0 and the slope is shallower ...