The R Book

Pattern Generation Resulting from Dynamic Interactions

In this section we look at an example of an ecological interaction between a species and its parasite. The interaction is unstable in a non-spatial model, with increasing oscillations in numbers leading quickly to extinction of the host species and then, in the next generation, its parasite. The non-spatial dynamics look like this:

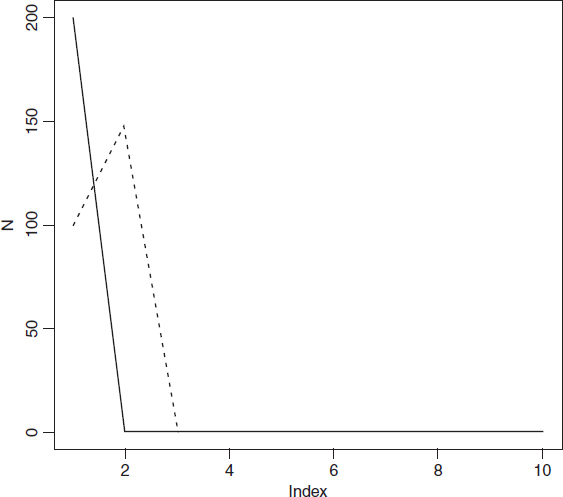
The parasite increases in generation number 1 and drives the host to extinction in generation 2, subsequently going extinct itself.

In a spatial model, we allow that hosts and parasites can move from the location in which they were born to any one of the eight first-order neighbouring cells (p. 819). For the purposes of dispersal, the universe is assumed have wrap-around margins for both species. The interaction is interesting because it is capable of producing beautiful spatial patterns that fluctuate with host and parasite abundance. We begin by setting the parameter values for the dynamics of the host (r) and the parasite (a) and the migration rates of the host (Hmr = 0.1) and parasite (Pmr = 0.9): in this case the hosts are relatively sedentary and the parasites are highly mobile:

r<-0.4
a<-0.1
Hmr<-0.1
Pmr<-0.9

Next, we set up the matrices of host (N) and parasite (P) abundance. These will form what is termed a coupled map lattice:

N<-matrix(rep(0,10000),nrow=100)
P<-matrix(rep(0,10000),nrow=100) ...