The R Book, 2nd Edition

Chapter 7

Mathematics

You can do a lot of maths in R. Here we concentrate on the kinds of mathematics that find most frequent application in scientific work and statistical modelling:

• functions;
• continuous distributions;
• discrete distributions;
• matrix algebra;
• calculus;
• differential equations.

7.1 Mathematical functions

For the kinds of functions you will meet in statistical computing there are only three mathematical rules that you need to learn: these are concerned with powers, exponents and logarithms. In the expression xb the explanatory variable is raised to the power b. In ex the explanatory variable appears as a power – in this special case, of e = 2.718 28, of which x is the exponent. The inverse of ex is the logarithm of x, denoted by log(x) – note that all our logs are to the base e and that, for us, writing log(x) is the same as ln(x).

It is also useful to remember a handful of mathematical facts that are useful for working out behaviour at the limits. We would like to know what happens to y when x gets very large (e.g. x → ∞) and what happens to y when x goes to 0 (i.e. what the intercept is, if there is one). These are the most important rules:

• Anything to the power zero is 1: x0 = 1.
• One raised to any power is still 1: 1x = 1.
• Infinity plus 1 is infinity: ∞ + 1 = ∞.
• One over infinity (the reciprocal of infinity, ∞–1) is zero: .
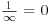• A number > 1 raised to the power infinity ...