GEOMETRIC RANDOM WALKS
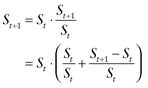
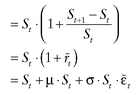
Get The Theory and Practice of Investment Management: Asset Allocation, Valuation, Portfolio Construction, and Strategies, Second Edition now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

