Theory and Methods of Statistics

1.10 Independent Random Variables and Conditioning When There Is Dependence

Random variables X₁, …, X_k are said to be mutually independent if

$\begin{array}{l}\hfill F_{X_1,\dots ,X_k}(x_1,\dots ,x_k)=\prod _{i=1}^k{F}_{X_i}(x_i)\text{for all}{x}_1,\dots ,x_k.\end{array}$

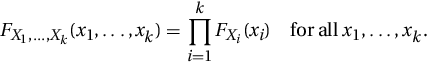  (8a)

Equivalently, for mutually independent rv’s,

$\begin{array}{l}\hfill f_{X_1,\dots ,X_k}(x_1,\dots ,x_k)=\prod _{i=1}^k{f}_{X_i}(x_i)\text{for all}{x}_1,\dots ,x_k,\end{array}$

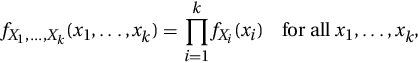  (8b)

holds for their joint pdf or joint pmf. The conditional pmf or pdf of X_r+1, …, X_k given (X₁, …, X_r) = (x₁, …, x_r) when $f_{X_1,\dots ,X_r}(x_1,\dots ,x_r)>0$ is

$\begin{array}{l}\hfill f_{(X_{r+1},\dots }\end{array}$