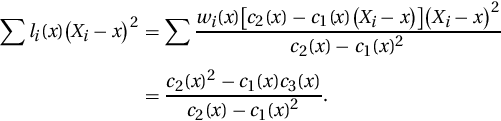
For any nonnegative integer r, using Chebychev’s inequality, it can be established that
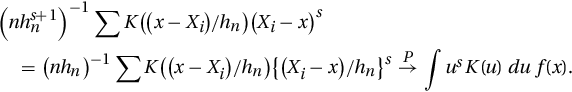
Noting that ![]() for s = 1 and s = 3 (since K is symmetric about 0), we have
for s = 1 and s = 3 (since K is symmetric about 0), we have
Plugging in these approximations for , , and in the expression ...
Get Theory and Methods of Statistics now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.

