April 2012
Intermediate to advanced
416 pages
10h 40m
English
Content preview from Theory of ComputationBecome an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.
4.4 NON CONTEXT FREE LANGUAGES; ANOTHER PUMPING LEMMA
In this section we prove a pumping lemma for CFL that is similar, but as expected from the richer structure of the PDA, more complex than the one for regular languages. We will benefit in our proof from the concept of parse tree for a CFG. The reader has most likely encountered trees in courses on discrete mathematics, data structures, etc. A tree is a structure like the one drawn below:
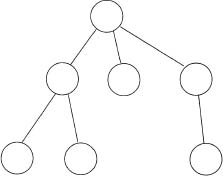
Since by default all edges point “downwards”, one does not need to emphasize so by drawing them as arrows. The round nodes may or may not have names. Our parse trees will have all their nodes named. The precise angle or slope of the edges does not matter—meaning, we allow variation in drawings without changing the tree we want to depict. However, left to right order matters, thus the following is a different tree from the one above. Our trees are ordered.
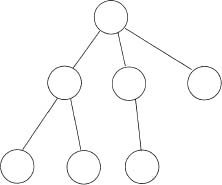
Of course, the reader has encountered many aspects of discrete mathematics before, but this did not stop me from reintroducing some such concepts in Chapter 1. So, let us revisit the definition of trees. A tree has both a “data” component (the node “contents”, whatever they may be) and a structural component or geometry, that is, how the nodes are interconnected. This motivates us to opt for ...
Become an O’Reilly member and get unlimited access to this title plus top books and audiobooks from O’Reilly and nearly 200 top publishers, thousands of courses curated by job role, 150+ live events each month,
and much more.
Read now
Unlock full access
More than 5,000 organizations count on O’Reilly
O’Reilly covers everything we've got, with content to help us build a world-class technology community, upgrade the capabilities and competencies of our teams, and improve overall team performance as well as their engagement.Julian F.
I wanted to learn C and C++, but it didn't click for me until I picked up an O'Reilly book. When I went on the O’Reilly platform, I was astonished to find all the books there, plus live events and sandboxes so you could play around with the technology.Addison B.
I’ve been on the O’Reilly platform for more than eight years. I use a couple of learning platforms, but I'm on O'Reilly more than anybody else. When you're there, you start learning. I'm never disappointed.Amir M.
I'm always learning. So when I got on to O'Reilly, I was like a kid in a candy store. There are playlists. There are answers. There's on-demand training. It's worth its weight in gold, in terms of what it allows me to do.